Question 1003617: Factor the trinomial 36x^2 +5x-50 into the form (Ax+B)(Cx+D) with A, B, C, and D integers, and A and B non-negative. Find the value of A+B+C+D.
Found 3 solutions by stanbon, MathTherapy, mp2019:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Factor the trinomial 36x^2 +5x-50 into the form (Ax+B)(Cx+D) with A, B, C, and D integers, and A and B non-negative. Find the value of A+B+C+D.
-----------
Use the AC Method to factor::
Note;
-45*40 = 36*-50 = -1800
45+40 = +5
----
Rewrite the trinomial as::
36x^2 -45x+40x - 50
----
Factor to get::
9x(4x-5)+10(4x-5)
------
(4x-5)(9x+10)
----
A + B + C + D = 4-5+9+10 = 18
--------
Cheers,
Stan H.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Factor the trinomial 36x^2 +5x-50 into the form (Ax+B)(Cx+D) with A, B, C, and D integers, and A and B non-negative. Find the value of A+B+C+D.
Factor the trinomial to get: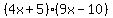 
A = 4
B = 5
C = 9
D = - 10
A + B + C + D = 4 + 5 + 9 - 10, or 
Answer by mp2019(1) (Show Source):
|
|
|
