Question 1003177: Find the domain and range of the following function in interval form.
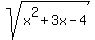 divided by divided by 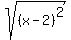
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The restrictions to the domain are
denominators cannot be zero, so 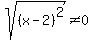 <--> <--> , and , and
expressions inside square roots cannot be negative, so  . .
(We know that  is not negative). is not negative).
 is negative for is negative for 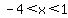 , ,
so ((-4,1) is not part of the domain,
and we knew that  is not part of the domain, either. is not part of the domain, either.
For any other value of  , ,  is defined, so is defined, so
the domain of  is is      . .
The function cannot be negative, because square roots are non-negative in their domain.
We know  for for  . .
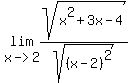 = =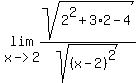 = =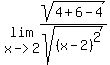 = =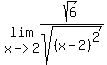   
Since  is continuous in is continuous in  , ,
 , and , and 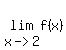    , ,
 takes all values from takes all values from  to to   in in  . .
The range of  in the interval in the interval  is is     . .
Whatever it does in the rest of its domain, it cannot be negative,
so the range of  across all of its domain is across all of its domain is     . .
|
|
|