Question 1002887: I have tried so many times to solve the problem
Find the exact value of
sin (x/2) = 2cos^2(x)-1
I've changed the sin (x/2) to the half angle identity and changed the 2cos^2(x)-1 to cos 2x, which is the double angle identity and tried to solve to be able to set everything to 0, but nothing I have tried worked. Please help as best as you can.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the exact value of
sin (x/2) = 2cos^2(x)-1
------------
The trig functions have to have the same argument.
sin^2(x/2) = (1 - cos(x))/2
----
sin(x/2) = 2cos^2(x)-1
Square both sides
sin^2(x/2) = 4cos^4(x) - 4cos^2(x) + 1
(1 - cos(x))/2 = 4cos^4(x) - 4cos^2(x) + 1
1 - cos(x) = 8cos^4(x) - 8cos^2(x) + 2
8cos^4(x) - 8cos^2(x) + cos(x) + 1 = 0
----------------
If you inspect
8x^4 - 8x^2 + x + 1 = 0 it's obvious that x = -1 is a zero.
--> cos(x) = -1
--> x = pi + n*2pi, n = ±0,1,2,3...
------------
Divide the quartic by (x+1)
--> 8x^3 - 8x^2 + 1 = 0
It's less obvious, x = 1/2 is a zero.
--> cos(x) = 0.5
--> x = pi/3 + n*2pi, n = ±0,1,2,3...
and
--> x = 2pi/3 + n*2pi, n = ±0,1,2,3...
-------------------------
Divide the cubic by (x - 1/2):
--> 8x^2 - 4x - 2 = 0
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=80 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 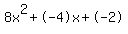 can be factored: can be factored:

Again, the answer is: 0.809016994374947, -0.309016994374947.
Here's your graph:
 |
======================
--> cos(x) = 
--> x = pi/5 + n*2pi, n = ±0,1,2,3...
--> x = 9pi/5 + n*2pi, n = ±0,1,2,3...
-----------------
and x = 3pi/5 + n*2pi, n = ±0,1,2,3...
and x = 7pi/5 + n*2pi, n = ±0,1,2,3...
|
|
|