SOLUTION: Given: Angle A is the vertex of an isosceles triangle. The number of degrees in angle B is twice the number of centimeters in segment BC. The number of degrees in angle C is three

Algebra ->  Triangles -> SOLUTION: Given: Angle A is the vertex of an isosceles triangle. The number of degrees in angle B is twice the number of centimeters in segment BC. The number of degrees in angle C is three       Log On


   

Question 1002463: Given: Angle A is the vertex of an isosceles triangle. The number of degrees in angle B is twice the number of centimeters in segment BC. The number of degrees in angle C is three times the number of centimeters in segment AB.
m angle b=x+6
m angle c=2x-54
Find: The perimeter of triangle ABC

At this point, I have no clue where to start. I've drawn the triangle with it's angles labeled but that's as much as I'm able to do.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625) About Me  (Show Source):
You can put this solution on YOUR website!

A diagram made to show Triangle ABC, A at top, B and C as base angle points. AB=AC and as given angle measure at B is 2*BC, and angle measure at C is 3*AB. The base angles are congruent which is to mean measure angle at B equals measure of angle at C.

The two relationships:
system%28AB=AC%2C2BC=3AB%29

Using that system of equations,
system%28AB=%282%2F3%29BC%2CAC=%282%2F3%29BC%29


Goal is to find perimeter.
AB%2BBC%2BAC
%282%2F3%29BC%2BBC%2B%282%2F3%29BC
%282%2F3%2B1%2B2%2F3%29BC
highlight%28%287%2F3%29BC%29

This seems the best that can be done. Something of this sort or another equivalent is what is possible. The problem description is not enough for a VALUE for the perimeter.
(POST-ADD: I believe misunderstood the data given AFTER the description, and did not use that as any data.)

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!

Given: Angle A is the vertex of an isosceles triangle. The number of degrees in angle B is twice the number of centimeters in segment BC. The number of degrees in angle C is three times the number of centimeters in segment AB.
m angle b=x+6
m angle c=2x-54
Find: The perimeter of triangle ABC

At this point, I have no clue where to start. I've drawn the triangle with it's angles labeled but that's as much as I'm able to do.
Angle C = 2x – 54 (given)

Angle C = 3(AB)

2x – 54 = 3AB

%282x+-+54%29%2F3+=+AB



Angle B = x + 6 (given)

Angle B = 2(BC)

x + 6 = 2BC

%28x+%2B+6%29%2F2+=+BC



With A being the vertex angle, angle B = angle C, OR

x + 6 = 2x – 54

x – 2x = - 54 – 6 

- x = - 60

x = 60



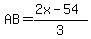
AB+=+%282x+-+54%29%2F3

AB+=+%282%2860%29+-+54%29%2F3

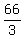AB+=+%28120+-+54%29%2F3, or 66%2F3, or 22 cm

AC also = 22 cm 

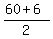BC+=+%28x+%2B+6%29%2F2, or %2860+%2B+6%29%2F2, or 66%2F2, or 33 cm



Perimeter: 2(22) + 33, or 44 + 33, or highlight_green%2877%29 cm