|
Question 1001766: What is the intersection of a cone and a plane parallel to a line along the side of the cone?
Provide mathematical examples to support your opinions. You may use equations, diagrams, or graphs to organize and present your thoughts.
Found 2 solutions by solver91311, KMST:
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!
If by "line along the side of the cone" you mean one of the generators of the cone, then the intersection is a parabola.
John
My calculator said it, I believe it, that settles it
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! The person asking the question has a meaning in mind for the expressions "a cone" and "a plane parallel to a line along the side of the cone".
Not knowing him/her, I cannot read that mind, so I must make some assumptions.
A straight line along the side of the cone must go through the vertex of the cone.
Let's place that cone on a 3D x-y-z coordinate space,
or rather, I will place x-, y-, and z-axes around that cone.
I will place the vertex at the origin,
the axis of the cone along the positive y-axis, and
the "line along the side of the cone" on the x-y plane.
The cross section of the cone with the line looks kind of like this:
 .
I assume that by cone we mean an infinite lateral surface,
with no base, or a base represented by  , if you wish.
I am not assuming that the infinite cone extends to any  .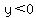
The equation of the line is  .
The equation for the cone would be  ,
and the z-axis is the axis that we do not see,
because it comes perpendicularly out of the screen towards us,
but at every  level, the "horizontal" section of the cone is a circle,
centered at the point with  ,
with radius  , such that  <---> .
Now, how could we place a plane parallel to that line?
The line is part of the plane  that is tangent to the cone's surface.
A plane parallel to that plane,  ,
is a plane that I would call parallel to the line .
That is probably what was envisioned in the question. I assume so.
The intersection of and
is obviously
 --> --> --> --> --> -->
and that equation does look like a parabola.
Of course, the intersection of the cone and plane is not on the x-z plane.
is just the projection of that parabolic intersection on the x-z plane.
The actual intersection is slightly stretched version of that projection.
We can keep the x-axis, but we need a new  axis.
That is the line  ,
and on that axis a   becomes a distance  ,
so the parabola is just a little stretched.
The line is also part of the plane  that contains the axis of the cone.
A plane parallel to that plane,  ,
is also a plane that I would call parallel to the line .
The intersection of and
is obviously  --> --> --> --> .
That is half of a hyperbola on the plane.
There is an infinite number of other planes that I could consider,
but I think of them as linear combinations of the planes already described.
|
|
|
| |
