SOLUTION: find the domain of the function. f(x)= ln(x^2-9 / x^2+9x+14)

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: find the domain of the function. f(x)= ln(x^2-9 / x^2+9x+14)      Log On


   

Question 1001695: find the domain of the function.

f(x)= ln(x^2-9 / x^2+9x+14)
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
You need to determine where the function under the logarithm,

f(x) = %28x%5E2-9%29%2F%28x%5E2+%2B+9x+%2B+14%29  is greater than zero,  f(x) > 0.

Notice that  1)  x%5E2-9%29= = (x+3)*(x-3),  and  2) 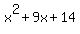 x%5E2+%2B+9x+%2B+14 = (x+2)*(x+7).     Therefore,

f(x) = 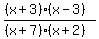%28%28x%2B3%29%2A%28x-3%29%29%2F%28%28x%2B7%29%2A%28x%2B2%29%29.

Now,  f(x) > 0

1)  in the semi-infinite interval  x < -7,  or 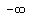 (-infinity, -7);

2)  in the interval  -3 < x < -2,  or  (-3, -2);

3)  in the semi-infinite interval  x > 3,  or  (3, infinity).

See the plots below.




Figure. Plot f(x) (red line);
plot of the numerator (green line);
plot of denominator (blue line).