Question 1001679:
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The angles of a pentagon are in a ratio of 7:6:5:5:4. Find the measures of each angle.
----------------------------------------------------------
This phrase "The angles of a pentagon are in a ratio of 7:6:5:5:4" means that there is a common measure, x, of all of these angles, such that
the 1-st angle is 7 times of this measure, 7x,
the 2-nd angle is 6 times of this measure, 6x,
the 3-rd angle is 5 times of this measure, 5x,
the 4-th angle is 5 times of this measure, 5x, and
the 5-th angle is 4 times of this measure, 4x.
The sum of internal angles of a pentagon is 180°*(5-2) = 540°,
so you have an equation to find this common measure:
7x + 6x + 5x + 5x + 4x = 540, or
27x = 540.
Hence, x = 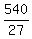 = 20°. = 20°.
Now you can determine the measure of each angle.
1-st angle is 7*20° = 140°,
2-nd angle is 6*20° = 120°,
and so on . . .
|
|
|