Question 1001620: A farmer builds a rectangular grid of pens with 1 row and 4 columns using 850 feet of fencing. What dimensions will maximize the total area of the pen?
Really confused on how to do this problem. Any help would be great!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!   of that rectangular row of pens. of that rectangular row of pens.
 ---> ---> ---> ---> ---> ---> ---> --->
The equation  shows that shows that  is a quadratic function of is a quadratic function of  . .
If we graphed it, it would be a parabola with a vertical axis
(parallel to the  axis), axis),
going through a maximum.
You may prefer to use variables/formats/formulas/recipes that are customary in algebra.
In that case you would call the width  and the total area of the pens and the total area of the pens  , ,
and you would write  <--> <--> . .
Then you would use the formula to find the maximum of a quadratic function:
 for the function for the function  . .
In this case  and and  so so
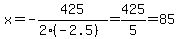 . .
WITHOUT FORMULAS:
If we graphed  as a function of as a function of  , ,
it would be a parabola with a vertical axis
(parallel to the  axis), axis),
going through a maximum.
We are trying to find the width  at that maximum. at that maximum.
 for for  and and  <--> <--> <--> <--> <--> <--> . .
Since parabolas are symmetrical, the axis (and vertex/maximum)
is halfway between  and and  at at  . .
For  , ,  . .
So, the dimensions that maximize total area are
 for the width of the row of pens, for the width of the row of pens,
 for the length of the row of pens, for the length of the row of pens,
and if you wanted the 4 pens to be of equal size, each pen would measure 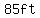 by by
 . .
|
|
|