What is the formula for this sequences of numbers?
60 50 40 30 20
First, check to see whether it is a geometric series, an
arithmetic series or neither:
Checking to see if it is a geometric series:
Divide the 2nd term by the 1st term: 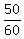 =
=  Divide the 3rd term by the 2nd term:
Divide the 3rd term by the 2nd term: 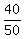 =
=  Divide the 4th term by the 3rd term:
Divide the 4th term by the 3rd term: 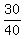 =
=  Divide the 5th term by the 4th term:
Divide the 5th term by the 4th term: 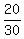 =
=  These are certainly not all the same. In fact, they are all different.
In fact, we could have stopped when we found that the 3rd term divided
by the 2nd term was not the same as the 2nd term divided by the first
term.
Therefore it is NOT a geometric series.
Checking to see if it is an arithmetic series:
Subtract: 2nd term minus 1st term:
These are certainly not all the same. In fact, they are all different.
In fact, we could have stopped when we found that the 3rd term divided
by the 2nd term was not the same as the 2nd term divided by the first
term.
Therefore it is NOT a geometric series.
Checking to see if it is an arithmetic series:
Subtract: 2nd term minus 1st term:  =
=  Subtract: 3rd term minus 2nd term:
Subtract: 3rd term minus 2nd term: 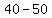 =
=  Subtract: 4th term minus 3rd term:
Subtract: 4th term minus 3rd term: 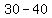 =
=  Subtract: 5th term minus 4th term:
Subtract: 5th term minus 4th term: 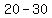 =
=  These ARE all the same.
So it IS an arithmetic series, with common difference, d=-10
The formula for the nth term of an arithmetic sequence is
an = a1 + (n-1)d
where a1 = first term = 60 and d = common difference = -10
Substituting:
an = 60 + (n-1)(-10)
an = 60 + (-10)(n-1)
an = 60 - 10n + 10
an = 70 - 10n
That's it! Checking:
Plug in n=1 and you get a1 = 70 - 10(1) = 70-10 = 60 = the 1st term.
Plug in n=2 and you get a2 = 70 - 10(2) = 70-20 = 50 = the 2nd term.
Plug in n=3 and you get a3 = 70 - 10(3) = 70-30 = 40 = the 3rd term.
Plug in n=4 and you get a4 = 70 - 10(4) = 70-40 = 30 = the 4th term.
Plug in n=5 and you get a5 = 70 - 10(5) = 70-50 = 20 = the 5th term.
So it checks.
Edwin
These ARE all the same.
So it IS an arithmetic series, with common difference, d=-10
The formula for the nth term of an arithmetic sequence is
an = a1 + (n-1)d
where a1 = first term = 60 and d = common difference = -10
Substituting:
an = 60 + (n-1)(-10)
an = 60 + (-10)(n-1)
an = 60 - 10n + 10
an = 70 - 10n
That's it! Checking:
Plug in n=1 and you get a1 = 70 - 10(1) = 70-10 = 60 = the 1st term.
Plug in n=2 and you get a2 = 70 - 10(2) = 70-20 = 50 = the 2nd term.
Plug in n=3 and you get a3 = 70 - 10(3) = 70-30 = 40 = the 3rd term.
Plug in n=4 and you get a4 = 70 - 10(4) = 70-40 = 30 = the 4th term.
Plug in n=5 and you get a5 = 70 - 10(5) = 70-50 = 20 = the 5th term.
So it checks.
Edwin