Question 1000288: Two man cycled towards each other distance of 200 km ,one from A and other from B.the first tourist left point A 6 hrs later than the 2nd left pt B, reached at same time find speed of faster
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE SITUATION AS PER MY INTERPRETATION OF THE WORDING:
The first tourist left point A, cycling towards point B, 6 hrs after a second tourist had left point B cycling towards point A. Both tourists reached their destination at the same time. The distance between points A and B is 200 km.
CONCLUSIONS:
The first tourist cycled at a faster average speed than the second tourist.
We do not have enough information to calculate the average speed of the first, faster tourist. (We cannot calculate the average speed of the second, slower tourist either).
EXPLANATION:
There are infinity of mathematically possible (although not necessarily plausible) answers.
We define variables like this:
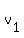 = average speed of the first tourist, in km per hour, = average speed of the first tourist, in km per hour,
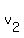 = average speed of the second tourist, in km per hour, and = average speed of the second tourist, in km per hour, and
 = time the first tourist spent cycling from A to B, in hours. = time the first tourist spent cycling from A to B, in hours.
From the wording of the problem we know that:
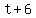 = time the second tourist spent cycling from B to A, in hours, = time the second tourist spent cycling from B to A, in hours,
 = distance cycled by the first tourist, in km, and = distance cycled by the first tourist, in km, and
 = distance cycled by the second tourist, in km. = distance cycled by the second tourist, in km.
Unfortunately, the system of equations  , ,
with 3 variables related by only 2 equations,
has an infinite number of solutions.
We can tabulate some of them:

Maybe the first tourist was Superman, and cycled for only 4 hours at 50 km per hour,
while the second tourist was a Tour de France pro, and covered the same 200 km in 10 hours, at a remarkable average speed of 20 km per hour.
Maybe the first tourist was that Tour de France pro, who covered the 200 km from point A to point B in 10 hours, at an average speed of 20 km per hour,
and the second tourist was an endurance athlete who managed to cover the same 200 km in 16 hours, at an average speed of 12.5 km per hour.
Since the possibilities are infinite, I cannot list or describe them all.
I just tabulated a few possibilities, and described only two.
|
|
|