Question 1000287: Two man cycled towards each other,one from A and other from B.the first tourist left point A 6 hrs later than the 2nd left pt B, reached at same time find speed of faster
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! No way to find a unique answer. Way too little information. We need at least two more pieces of information.
We could not even find a unique answer if the distance between A and B was given as in the problem below:
"One tourist left point A, cycling towards point B, 6 hrs after a second tourist had left point B cycling towards point A. Both tourists reached their destinations at the same time. The distance between points A and B is 200 km".
In that case, we could define variables, translate the information into equations,
and we would still need an extra equation to be able to find a unique answer:
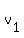 = average speed of the first tourist, in km per hour. = average speed of the first tourist, in km per hour.
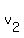 = average speed of the second tourist, in km per hour. = average speed of the second tourist, in km per hour.
 = time the first tourist spent cycling from A to B, in hours. = time the first tourist spent cycling from A to B, in hours.
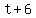 = time the second tourist spent cycling from B to A, in hours. = time the second tourist spent cycling from B to A, in hours.
 = distance cycled by the first tourist, in km. = distance cycled by the first tourist, in km.
 = distance cycled by the second tourist, in km. = distance cycled by the second tourist, in km.
Unfortunately, the system of equations  , ,
with 3 variables related by only 2 equations,
has an infinite number of solutions.
We can tabulate some of them:

Since the possibilities are infinite, I cannot list or describe them all.
|
|
|