Question 1000285: Two indian tourists in US cycled towards each other,one from A and other from B.the first tourist left point A 6 hrs later than the 2nd left pt B, and it turned out on their meeting that he had travelled 12 km less than the second tourist. After meeting,they kept cycling with the same speed, and the first tourist arrived at B 8 hours later and the 2nd arrived at A 9 hours later. Find speed of the faster tourist
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Both tourists meet at point C, located somewhere between A and B.
The first tourist cycles for  hours at an average speed of hours at an average speed of 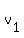 km/hour, going from A to C. km/hour, going from A to C.
So the distance from A to C is
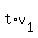 . .
After the two tourists meet at C, the second tourist cycles from C to A,
at an average speed of 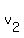 km/hour, for km/hour, for  hours. hours.
So the distance from C to A is
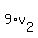 . .
Since the the distance from A to C is the same as the distance from C to A,
 (equation 1). (equation 1).
The second tourist cycled from B to C in 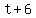 hours, at an average speed of hours, at an average speed of 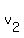 km/hour. km/hour.
So the distance from B to C is
 . .
After the two tourists meet at C, the second tourist cycles from C to B,
at an average speed of 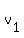 km/hour, for km/hour, for  hours. hours.
So the distance from C to A is
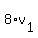 . .
Since the the distance from B to C is the same as the distance from C to B,
 (equation 2). (equation 2).
Dividing equation 2 by equation 1, we get
 ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> --->
From there, we conclude that
 ---> ---> , because , because  ---> ---> does not make sense. does not make sense.
Then  . .
Substituting  into equation 1, we get into equation 1, we get
 ---> ---> . .
Before they met at C,
the second tourist had cycled  ,while ,while
the first tourist had cycled  . .
Since the first tourist had traveled 12 km less than the second tourist,
 ---> ---> ---> ---> . .
 ---> ---> ---> ---> ---> ---> ---> ---> . .
Then  ---> ---> ---> ---> ---> --->
|
|
|