|
Question 656372: x^4/3 = 256
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!
The solution to this problem will have the form:
x = something
The exponent on this "x" is a 1. So one way to solve this problem is to figure out how to turn the exponent we have, 4/3, into the exponent we want, 1. We have several rules for exponents which show us how exponents can be changed. The rule we need is the power of a power rule. We will raise both sides of the equation by the same power so that the exponent on the left turns into a 1:
The question now is, what should "n" be in order for the exponent on the left to turn into a 1? The rule tells us that we should multiply these exponents. So 4/3 times what number results in a 1? Since the product of all reciprocals is a 1, we can use the reciprocal of 4/3, which is 3/4, to get the desired exponent:
On the left we get what we wanted, x. All that remains is to simplify the right side as much as possible. If you have trouble with fractional or negative exponents, I find that it can help if you factor the exponent in a special way:- If the exponent is negative, factor out -1.
- If the exponent is a fraction with an exponent that is not 1, then factor out the numerator.
Our exponent of 3/4 is not negative. But it is a fraction whose numerator is not a 1. So we will factor out the numerator:
Each factor tells us an operation to perform. The factor of 3 tells us that we will cube a number and the factor of 1/4 (if you remember your fractional exponents) means find a 4th root. An advantage of factoring the exponent is that these operations can be done in any order. We can cube 256 first and then find a 4th root:
or we can find a 4th root first and then cube it:
With a little investigation we can find that 256 is 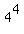 . So a 4th root is not hard to find. In fact it will be easier to find the 4th root of 256 than it will be to find the 4th root of 356 cubed. So we will find the 4th root first:
And cubing 4 is simple:
|
|
|
| |
