SOLUTION: A rectangle is 4 times as long as it is wide. A second rectangle is 5 centimeters longer and 2 centimeters wider than the first. The area of the second rectangle is 270 square cent

Algebra ->  Customizable Word Problem Solvers  -> Unit conversion -> SOLUTION: A rectangle is 4 times as long as it is wide. A second rectangle is 5 centimeters longer and 2 centimeters wider than the first. The area of the second rectangle is 270 square cent      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 285614: A rectangle is 4 times as long as it is wide. A second rectangle is 5 centimeters longer and 2 centimeters wider than the first. The area of the second rectangle is 270 square centimeters greater than the first. What are the dimensions of the original rectangle?
I would like to see how to solve the problem in steps, if possible. Thank you!
Found 2 solutions by JBarnum, MathTherapy:
Answer by JBarnum(2146) About Me  (Show Source):
You can put this solution on YOUR website!
A=LW, A=5L because w=4l. A=LW is the first rectangle
W=4L "A rectangle is 4 times as long as it is wide."
X=L%2B5 Y=W%2B2 "A second rectangle is 5 centimeters longer and 2 centimeters wider than the first."
XY=A%2B270 "The area of the second rectangle is 270 square centimeters greater than the first" this is the second rectangle.
so now wee need to substitute to be able to solve for L
XY=A%2B270
%28L%2B5%29%28W%2B2%29=5L%2B270
%28L%2B5%29%284L%2B2%29=5L%2B270
%284L%5E2%2B20L%2B2L%2B8%29=5L%2B270
4L%5E2%2B22L-5L%2B8-270=0
4L%5E2%2B17L-262=0
use the quadratic formula to solve for L, below is the solver to show steps, but for now L=6.24orL=-10.49 but the lengths cant be negative so L=6.24
now we can find all the other lengths of the 2 rectangles
first rectangle:
A=LW
A=6.24%2824.96%29
A=155.7504


W=4L
W=4%286.24%29
W=24.96
___________
X=L%2B5
X=%286.24%29%2B5
X=11.24
___________
Y=W%2B2
Y=%2824.96%29%2B2
Y=26.96

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation aL%5E2%2BbL%2Bc=0 (in our case 4L%5E2%2B17L%2B-262+=+0) has the following solutons:

L%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2817%29%5E2-4%2A4%2A-262=4481.

Discriminant d=4481 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-17%2B-sqrt%28+4481+%29%29%2F2%5Ca.

L%5B1%5D+=+%28-%2817%29%2Bsqrt%28+4481+%29%29%2F2%5C4+=+6.24253398558978
L%5B2%5D+=+%28-%2817%29-sqrt%28+4481+%29%29%2F2%5C4+=+-10.4925339855898

Quadratic expression 4L%5E2%2B17L%2B-262 can be factored:
4L%5E2%2B17L%2B-262+=+4%28L-6.24253398558978%29%2A%28L--10.4925339855898%29
Again, the answer is: 6.24253398558978, -10.4925339855898. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+4%2Ax%5E2%2B17%2Ax%2B-262+%29

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

Let the width of the 1st rectangle be W. Then its length = 4W, since its length is 4 times its width

The width and length of the 2nd rectangle are W + 2, and 4W + 5, respectively, since the second rectangle is 2 centimeters wider and 5 centimeters longer than the 1st.

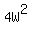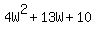The area of the 1st rectangle is then: W*4W, or 4W%5E2, and the area of the 2nd rectangle is (W + 2)(4W + 5 ), or 4W%5E2+%2B+13W+%2B+10%29.

Since the area of the 2nd rectangle is 270 square centimeters greater than the area of the 1st rectangle, then we’ll have:
4W%5E2+%2B+270+=+4W%5E2+%2B+13W+%2B+10
4W%5E2+-+4W%5E2+-+13W+=+10+-+270
- 13W = - 260
W+=+%28-260%29%2F-13+=+20

Now, since W, or width = 20, then the dimensions of the 1st rectangle are: W, or width = highlight_green%2820%29 cm, and L, or length = highlight_green%2880%29 cm ------> 4W, or 4(20)
Check:
Width of 1st rectangle = 20 cm
Length of 1st rectangle = 4(20) = 80 cm

Area of 1st rectangle = 20 * 80 = 1,600 sq centimeters

Width of 2nd rectangle = 22 cm (20 + 2)
Length of 2nd rectangle = 85 cm (4*20 + 5)

Area of 2nd rectangle = 22 * 85 = 1,870 sq centimeters

Area of 2nd rectangle (1,870 sq centimeters) is 270 sq centimeters greater than area of 1st rectangle (1,600 sq centimeters).

Send comments and “thank yous” to MathMadEzy@aol.com