Question 1185855: Two runners are running on circular tracks each of which has a circumference of
1320 feet. The tracks are 100 feet apart and the runners start opposite each
other and move at the same constant rate of 880 ft/min. How fast are the runners
separating when each has run 165 feet?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
>>>Two runners are running on circular tracks each of which has a circumference
of 1320 feet. The tracks are 100 feet apart...
Does that mean their closest points are 100 feet apart?
>>>...and the runners start opposite each other...
Does that mean they are 100 feet apart, or at corresponding points on the
tracks?
>>>...and move at the same constant rate of 880 ft/min.
Are they both running the same direction, clockwise or counterclockwise, or is
one running clockwise and the other counterclockwise? That will make a
difference.
This is a related rates calculus problem. We could do it for all possibilities,
but to avoid waste, why not make it totally clear and repost?
Edwin
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
I fully agree with Edwin in that the problem has too many uncertainties in its formulation.
The problem's formulation is at the amateur's level, not at the professional level.
More accurate formulations would be like this:
Two runners are running on circular tracks each of which has a circumference of
1320 feet. The tracks are 100 feet apart (the closest distance). The runners start
simultaneously from two closest points on the circles. One runner runs clockwise;
the other runner runs anti-clockwise. They move at the same constant rate of 880 ft/min.
How fast are the runners separating when each has run 165 feet?
The solution is quite simple.
First, notice that 165 feet is 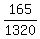 =  of the full circumference.
We can imagine that the centers of the circles are located on x-axis of a coordinate plane.
When the runners move 165 feet each, their corresponding position vectors will be
in position 45° and 135° to x-axis. So, the vectors of their speeds will be
u = (880*cos(45°),880*sin(45°)) for one runner,
and
v = (880*cos(135°),880*sin(135°)) for the other runner.
The difference of these vectors is u-v, i.e.
(880*cos(45°)-880*cos(135°),0).
So, the separating speed is  , or approximately 880*1.4142 = 1244.5 ft/minute.
At this point, the problem is just solved completely.
ANSWER. The separation speed is = 1244.5 ft/minute.
Solved.
Notice that I solved the problem without using Calculus, despite of the Edwin' suggestion.
|
|
|
