Question 1171404: Hi
Town P and town Q are 720km apart.Maggie & Andrew left town P at the same time. The average speed of Andrew was 40km per hour, Maggies was 60km per hour. As soon as they passed Point K which was 1/3 of the total distance,Maggie began to travel at a speed of 80km per hour. Both of them took the same number of hours to travel from town P to town Q.
How long did Maggie take to travel from town P to Point K.
What was Andrews speed from Point K to town Q.
Thanks
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is NOT a complete solution:
To reach point K, Maggie went 60 km per hour and distance  km. The time taken was km. The time taken was  hours. Maggie at point K was still 480 k.m. from point Q. hours. Maggie at point K was still 480 k.m. from point Q.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Town P and town Q are 720km apart.Maggie & Andrew left town P at the same time. The average speed of Andrew was 40km
per hour, Maggies was 60km per hour. As soon as they passed Point K which was 1/3 of the total distance, Maggie began
to travel at a speed of 80km per hour. Both of them took the same number of hours to travel from town P to town Q.
How long did Maggie take to travel from town P to Point K.
What was Andrews speed from Point K to town Q.
Thanks
It’s OBVIOUS that not only did Maggie increase her speed after getting to Point K, but Andrew did, as well.
Distance Maggie covered, from Point P to Point K:  of the 720-km distance: of the 720-km distance: 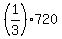 = 240 kms
Time Maggie took to get to Point K (240 kms): = 240 kms
Time Maggie took to get to Point K (240 kms):  = 4 hours
Remaining distance Maggie had to go (Point K to Q): 720 - 240 = 480 kms
Time Maggie took to go remaining distance (point K to Q), after increasing speed to 80 km/h: = 4 hours
Remaining distance Maggie had to go (Point K to Q): 720 - 240 = 480 kms
Time Maggie took to go remaining distance (point K to Q), after increasing speed to 80 km/h: 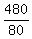 = 6 hours
Total time Maggie took to get from Point P to Q: 4 + 6 = 10 hours
Distance Andrew covered, from Point P to Point K: = 6 hours
Total time Maggie took to get from Point P to Q: 4 + 6 = 10 hours
Distance Andrew covered, from Point P to Point K:  of the 720-km distance: of the 720-km distance: 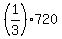 = 240 kms
Time Andrew took to get to Point K (240 kms): = 240 kms
Time Andrew took to get to Point K (240 kms):  = 6 hours
Remaining distance Andrew had to go (Point K to Q): 720 - 240 = 480 kms
Time Andrew took to go remaining distance (point K to Q), after increasing speed (S): = 6 hours
Remaining distance Andrew had to go (Point K to Q): 720 - 240 = 480 kms
Time Andrew took to go remaining distance (point K to Q), after increasing speed (S):  hours
Total time Andrew took to get from Point P to Q: hours
Total time Andrew took to get from Point P to Q: 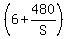 hours
Since BOTH took the same amount of time to travel from P to Q, then each took 10 hours to complete the trip
We then get: Andrew’s ENTIRE-TRIP time = Maggie’s ENTIRE-TRIP time hours
Since BOTH took the same amount of time to travel from P to Q, then each took 10 hours to complete the trip
We then get: Andrew’s ENTIRE-TRIP time = Maggie’s ENTIRE-TRIP time

 ----- Factoring out GCF, 2, in numerator
3S + 240 = 5S ---- Multiplying by LCD, S
240 = 5S - 3S
240 = 2S ===> 2S = 240
Andrew’s speed from K to Q, or ----- Factoring out GCF, 2, in numerator
3S + 240 = 5S ---- Multiplying by LCD, S
240 = 5S - 3S
240 = 2S ===> 2S = 240
Andrew’s speed from K to Q, or 
|
|
|