Question 1166905: A kayaker was paddling due East at 3mph and an orca was swimming due North at 10mph. If they started 1 mile apart, how long did it take for the orca to swim underneath the kayaker? Model this problem with an algebraic equation. Show work!
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A kayaker was paddling due East at 3mph and an orca was swimming due North at 10mph.
If they started 1 mile apart, how long did it take for the orca to swim underneath the kayaker?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let 't' be the time under the problem's question.
To get the meeting point, the kayaker paddled 3t miles to the east.
while the orca swam 10t miles to the North.
According to the problem, these distances, 3t miles and 10t miles,
are the legs of a right-angled triangle, whose hypotenuse is 1 mile.
So, we write the Pythagorean equation
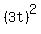 + + 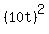 = 1, = 1,
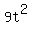 + + 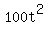 = 1, = 1,
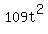 = 1, = 1,
 = = 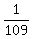 ,
t = ,
t = 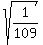 = 0.095782629 of an hour, or 0.095782629*60 = 5.746957711 minutes.
ANSWER. The time is about 5.747 minutes. = 0.095782629 of an hour, or 0.095782629*60 = 5.746957711 minutes.
ANSWER. The time is about 5.747 minutes.
Solved.
This problem is nice and interesting.
You can solve it considering the events in reverse time, assuming that the kayaker and the orca
move in perpendicular directions back from the meeting point to their starting positions.
Then after t hours the distance between them will be 1 mile,
and from this condition it is easy to find time 't'.
Thus we have simple, elegant and unexpectedly short solution.
|
|
|