Question 998846: On an upstream trip, a canoe travels 40 km in 5 hours. Downstream, it travels the same distance in half the time. What is the rate of the canoe in still water and the rate of the current?
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
On an upstream trip, a canoe travels 40 km in 5 hours. Downstream, it travels the same distance in half the time.
What is the rate of the canoe in still water and the rate of the current?
-------------------------------------------------------------------
On an upstream trip, the canoe speed relative to the river banks is 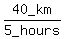 = 8 = 8  . .
This speed is the difference of the speed of canoe relative water, u, and the speed of current, v:
8 = u - v. (1)
Downstream, the canoe speed relative to the river banks is twice more: 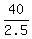 = 16 = 16  . .
This speed is the sum of the speed of canoe relative water, u, and the speed of current, v:
16 = u + v. (2)
Add (1) and (2). You will get
2u = 8 + 16 = 24, hence, u =  = 12 = 12  . .
Then v = 4  . .
Answer. The canoe speed in a still water is 12  . .
The current speed is 4  . .
|
|
|