SOLUTION: A plane flies 435 miles in the wind and 345 miles against the wind in the same length of time. If the speed of the wind is 15 miles per hour, find the speed of the plane in still

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: A plane flies 435 miles in the wind and 345 miles against the wind in the same length of time. If the speed of the wind is 15 miles per hour, find the speed of the plane in still      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 994774: A plane flies 435 miles in the wind and 345 miles against the wind in the same length of time. If the speed of the wind is 15 miles per hour, find the speed of the plane in still air
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
This is a very common form of uniform travel rates exercise. The solution here will be generalized.

RT=D relates rate (or speed), time, and distance.

VARIABLES

Direction           speed            time         distance
WITHWIND            r+w               t            D
AGAINSTWIND         r-w               t            d

Find the two expressions, formulas, for t.
Direction           speed            time         distance
WITHWIND            r+w              D/(r+w)       D
AGAINSTWIND         r-w              d/(r-w)       d

Those two times were given as equal.
highlight%28D%2F%28r%2Bw%29=d%2F%28r-w%29%29
The only unknown variable in this equation is r, the rate of the vehicle in still air.

SOLUTION STEPS FOR THE ARITHMETIC
D%28r-w%29=d%28r%2Bw%29
Dr-Dw=dr%2Bdw
Dr-dr-Dw=dw
Dr-dr=dw%2BDw
%28D-d%29r=dw%2BDw
highlight%28highlight%28r=%28dw%2BDw%29%2F%28D-d%29%29%29

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

A plane flies 435 miles in the wind and 345 miles against the wind in the same length of time. If the speed of the wind is 15 miles per hour, find the speed of the plane in still air
Let speed of the plane, in still air be S

Then speed of plane, with a tailwind = S + 15

Speed of plane, with a headwind = S – 15

We then form the following TIME equation: 435%2F%28S+%2B+15%29+=+345%2F%28S+-+15%29

435(S - 15) = 345(S + 15) ------- Cross-multiplying

435S - 6,525 = 345S + 5,175

435S – 345S = 5,175 + 6,525

90S = 11,700

S, or speed of plane in still air = 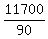11700%2F90, or highlight_green%28130%29 mph