SOLUTION: a cyclist rides her bike over a route that is 1/3 uphill, 1/3 level, and 1/3 downhill. If she covers the uphill part of the route at a rate of 16 km/h, and the level part at a rate

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: a cyclist rides her bike over a route that is 1/3 uphill, 1/3 level, and 1/3 downhill. If she covers the uphill part of the route at a rate of 16 km/h, and the level part at a rate      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 933374: a cyclist rides her bike over a route that is 1/3 uphill, 1/3 level, and 1/3 downhill. If she covers the uphill part of the route at a rate of 16 km/h, and the level part at a rate of 24 km/h, what rate would she have to travel during the downhill part of the route in order to average 24 km/h for the entire route?
(ANS: 48km/h)
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
RT=D, T=D/R.


__________________rate__________time__________distance
UP________________16____________(___)__________d/3
LEV_______________24___________(____)__________d/3
DWN_______________(___)________(____)__________d/3
Total__________________________(____)__________d



__________________rate__________time__________distance
UP________________16____________(d/(3*16))__________d/3
LEV_______________24___________(d/(3*24))__________d/3
DWN_______________(r)________(d/(3r))__________d/3
Total__________________________(____)__________d


The total time would be d%281%2F%283%2A16%29%2B1%2F%283%2A24%29%2B1%2F%283r%29%29; which needs simplification before comfortably using this expression. The AVERAGE speed would be d%2F%28d%281%2F%283%2A16%29%2B1%2F%283%2A24%29%2B1%2F%283r%29%29%29
1%2F%281%2F%283%2A16%29%2B1%2F%283%2A24%29%2B1%2F%283r%29%29=24;
LCD is 3*2*2*2*2, 3*2*2*2*3, 3*r,------highlight_green%283%2A3%2A2%2A2%2A2%2A2%2Ar%29;
---
Another way to continue is use reciprocals of both members.
-
1%2F%283%2A16%29%2B1%2F%283%2A24%29%2B1%2F%283r%29=1%2F24
Now multiply both members by LCD.
%283%5E2%2A2%5E4%2Ar%29%281%2F%283%2A16%29%2B1%2F%283%2A24%29%2B1%2F%283r%29%29=144r%2F24
3r%2B2r%2B48=6r
5r%2B48=6r
highlight%28r=48%29

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
d= 1/3 of the total route distance, in km, and
3d= the total route distance, in km.
Average time for the whole route =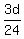3d%2F24 hours.
The time spent cycling uphill was 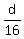d%2F16 hours, and
the time spent cycling on level was d%2F24 hours.
So, the time spent cycling downhill must have been
3d%2F24-d%2F16-d%2F24=6d%2F48-3d%2F48-2d%2F48=%286d-3d-2d%29%2F48=d%2F48 hours.
Then, the average speed in km/h cycling uphill for 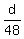d km in d%2F48 hours was
d%2F%22%28+d+%2F+48+%29%22=d%2848%2Fd%29=highlight%2848%29 .

CHECKING:
Let's say that the total route is 48%2A3=144 km.
That means 48 km cycling downhill, at 48 km/h, during 1 hour,
48 km cycling on level ground, at 24 km/h, during 2 hours, and
48 km cycling uphill, at 16 km/h, during 3 hours,
for a total of 48%2A3=144 km covered in 1%2B2%2B3=6 hours,
at an average rate of 48%2A3%2F6=24 km/h.