Question 930764: A and B start together from the same point on a circular track and walk in the same direction till they both again arrive together at the starting point. A completes one circle in 224 s and B in 364 s. How many times will A have passed B?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! For A and B to arrive together at the starting point,
each of them must have completed an integer number of turns.
The time (in seconds) required for that must be a multiple of 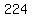 and of and of 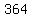 . .
 and and  , so , so
the minimum common multiple of 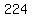 and and 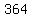 is is
 . .
That means that A and B first arrive together at the starting point 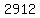 seconds after the start. seconds after the start.
During that time, A will have run  laps, laps,
and  will have run will have run  laps. laps.
Each time the distance A has run exceeds the distance B has run by an integer (1, 2, 3, or 4 laps), A is passing B.
When both have run for 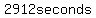 , A has run , A has run  more laps than B, and they are both arriving together at the starting point. more laps than B, and they are both arriving together at the starting point.
I do not count that time as A passing B,
because they both stop running at that point,
so A passes B 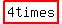 . .
A MORE DYNAMIC VIEW (in case you do not visualize it yet):
During their run, A is running at a speed of 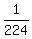 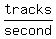 , ,
while B is running at a speed of 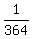 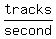 . .
The difference in the distance they have both covered increases at a rate of
 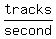 , ,
which means  . .
A will be passing B for the first time when he has run 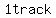 more than B, more than B,
which will take   . .
When they meet at the starting point, after 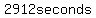 , A will have run , A will have run
 more than B, more than B,
meaning that A will pass B  during the during the 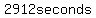 they both run before meeting again they both run before meeting again
|
|
|