Question 919886: Towns A and B are 540km apart. A train leaves A and travels to B at a constant speed. A second train leaves A 1h later and, after 2h, reaches a point passed by the first train 40min earlier. The second train then increases speed by 5km/h and arrives at B at the same time as the first train. What were the speeds of the trains when they left A?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Towns A and B are 540km apart.
A train leaves A and travels to B at a constant speed.
A second train leaves A 1h later and, after 2h, reaches a point passed by the first train 40min earlier.
The second train then increases speed by 5km/h and arrives at B at the same time as the first train.
What were the speeds of the trains when they left A?
:
A-----------------p-----------540 km-----------------------------B
:
1st train got to p in 3 hr - 40 min or 2 hrs hrs
2nd train got to p in 2 hrs, (after leaving 1 hr later than the 1st train)
We can say that 2nd train travels the same dist in 2 hrs, as the 1st train in 2 hrs, hrs,
time ratio; 1st train to 2nd train 2.33:2 or in integers 7:6 ratio
:
let s = speed of the 1st train
then
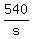 = travel time of the 1st train = travel time of the 1st train
:
speed varies inversely with time therefore
 s = initial speed of 2nd train s = initial speed of 2nd train
and
( s + 5) = 2nd train speed from p to B s + 5) = 2nd train speed from p to B
The distance to p (dist = speed * time) = 2* s = s = 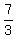 s s
:
2nd trains time to p = 3 hrs after the 1st train started
Write a time equation
3 hrs to p + time traveling from p to B = 1st train travel time
3 +  = = 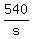
It's such a pain in the you know what, to deal with these fractions, try to use decimals and see what we get
3 +  = = 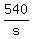
multiply by s(1.167s+5)
3s(1.167s+5) + s(540-2.33s) = 540(1.167s+5)
3.5s^2 + 15s + 540s - 2.33s^2 = 630s + 2700
Combine like terms
3.5s^2 - 2.33s^2 - 630s + 15s + 540s - 2700 = 0
1.167s^2 - 75s - 2700 = 0
using the quadratic formula, I got a postive solution of
s = 90 km/hr is the speed of the 1st train
then
 *90 = 105 km/hr, initial speed of the 2nd train *90 = 105 km/hr, initial speed of the 2nd train
:
:
Let's see if we lucked out and got this right, find the times.
1st train travel time = 540/90 = 6 hrs
2nd train travel time to p
2 * 105 = 210 km to p
2nd train speed to B = 110 km/hr (5 km/hr more)
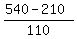 = 3 hrs = 3 hrs
2nd train total time
1 hr before starting
2 hrs to p
3 hrs p to B
------------
6 hrs, same as 1st train!!!
|
|
|