SOLUTION: A jet plane, flying 110 mph faster than a propeller plane, travels 5280 miles in 4 hours less time than the propeller plane takes to fly the same distance. How fast does each plane

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: A jet plane, flying 110 mph faster than a propeller plane, travels 5280 miles in 4 hours less time than the propeller plane takes to fly the same distance. How fast does each plane      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 833372: A jet plane, flying 110 mph faster than a propeller plane, travels 5280 miles in 4 hours less time than the propeller plane takes to fly the same distance. How fast does each plane fly?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39614) About Me  (Show Source):
You can put this solution on YOUR website!
Let r = speed for the propeller plane
Let h = time in hours for propeller plane to go 5280 miles distance


_____________speed_________________time_______________distance
JET__________r+110_________________h-4________________5280
PROP_________r_____________________h__________________5280


JET: %28r%2B110%29%28h-4%29=5280
rh%2B110h-4r-440=5280, and since rh=5280 we may substitute,
rh%2B110h-4r-440=rh
110h-4r-440=0

PROPELLER: rh=5280, and then h=5280/r
Using this, and returning to the JET equation,
-
JET (Returning to):
110%285280%2Fr%29-4r-440=0
110%2A5280-4r%5E2-440r=0
-4r%5E2-440r%2B110%2A5280=0
4r%5E2%2B440r-110%2A5280=0
r%5E2%2B110r-110%2A1320=0
highlight_green%28r%5E2%2B110r-145200=0%29
--
Still, unfinished. Use the general solution to a quadratic equation to solve for r. You can then simply compute r+110 for the jet plane.
Note:
(1) Once getting r, you can also find the time for travel of each plane.
(2) This exercise would be really nicely solved purely in symbolic form, meaning all in variables, not showing specific values. At least a few of this kind or form of exercise has been asked in the past few days on the site.

Answer by MathTherapy(10549) About Me  (Show Source):
You can put this solution on YOUR website!
A jet plane, flying 110 mph faster than a propeller plane, travels 5280 miles in 4 hours less time than the propeller plane takes to fly the same distance. How fast does each plane fly?


Let propeller plane's speed = S

Then jet plane's speed = S + 110

Propeller plane's time to travel 5,280 miles: 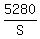5280%2FS

Jet plane's time to travel 5,280 miles: 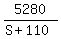5280%2F%28S+%2B+110%29

Since jet plane takes 4 hours less, then we can say that:

5280%2FS+-+4+=+5280%2F%28S+%2B+110%29 

5280(S + 110) - 4(S)(S + 110) = 5280S ----- Multiplying by LCD, S(S + 110)

5280S+%2B+580800+-+4S%5E2+-+440S+=+5280S

4S%5E2+%2B+440S+-+580800+=+0

4%28S%5E2+%2B+110S+-+145200%29+=+4%280%29 ----- Factoring out GCF, 4

S%5E2+%2B+110S+-+145200+=+0

(S - 330)(S + 440) = 0

S = 330               OR             S = - 440 (ignore)

S, or speed of propeller plane, for 5,280 miles = highlight_green%28330%29 mph

Speed of jet plane, for 5,280 miles: 330 + 110, or highlight_green%28440%29 mph

You can do the check!! 



If you need a complete and detailed solution, let me know!!



Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.

Further help is available, online or in-person, for a fee, obviously.