SOLUTION: Jenna went on a 90 mile trip to a soccer game. On the way back, due to road construction she had to drive 25 miles per hour slower. This made the trip take 15 hours longer. How fas

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: Jenna went on a 90 mile trip to a soccer game. On the way back, due to road construction she had to drive 25 miles per hour slower. This made the trip take 15 hours longer. How fas      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 818369: Jenna went on a 90 mile trip to a soccer game. On the way back, due to road construction she had to drive 25 miles per hour slower. This made the trip take 15 hours longer. How fast did she drive to the soccer game?
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
r = rate going TO the soccer game.

WAY___________speed___________time___________distance
GOING_________r_______________(___)__________90
RETURNING_____r-25____________(___)__________90

R*T=D means same as T=D/R so you fill in the missing time information:

WAY___________speed___________time___________distance
GOING_________r_______________90/r__________90
RETURNING_____r-25____________90%2Fr%2B15__________90

Both distances are the same, 90 miles. Letting y = 90/r, then time to return is y+15. I chose such a new variable assignment because of finding redundancy in possible equations. Equating the RT expressions for the 90 mile distance would be of no help.
Going, highlight%28r%2Ay=90%29
Returning, highlight%28%28r-25%29%28y%2B15%29=90%29
Simplifying the Returning equation, ry-25y%2B15r-25%2A15=90, and seeing already ry=90 allows a substitution:
90-25y%2B15r-25%2A15=90
15r-25y-375=0
Divide by 5:
3r-5y-75=0

We now have a system of two equations in variables r and y.
SYSTEM:
-----------------------
ry=90
-------------------
3r-5y=75
---------------------


That system will likely lead to a quadratic equation. Expected not to be tricky; substitution is useful to solve this for r and y.
Somehow, the question should be easier or simpler than this, but this system found should work.
(Tell me if you find difficulty from here.)

________________
Second time trying to post this solution because it did not appear...
From the system shown,
3r-5%2890%2Fr%29=75 by substitution using the "xy" equation,
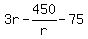
3r-450%2Fr-75
r-150%2Fr-25=0
r%5E2-150-25r=0
r%5E2-25r-150=0 not factorable.
General Solution to Quadratic:
r=%2825%2Bsqrt%2825%5E2-4%28150%29%29%29%2F2
r=%2825%2Bsqrt%28625%2B600%29%29%2F2
r=%2825%2Bsqrt%2825%2A49%29%29%2F2
r=%2825%2B5%2A7%29%2F2
highlight%28r=30%29 miles per hour

-----------------------
FURTHER NOTE:
Assigning the extra variable, y for time, was not in fact necessary.
From the Returning row of data, RT=D, find that %28r-25%29%2890%2Fr%2B15%29=90, all in only the one variable, r.
Performing the multiplications and simplifying, you should obtain the equation, r%5E2-25r-150=0, the very same quadratic equation found in the previous solution.