Question 72551: 18. A passenger train can travel 325 mi. in the same time a freight train takes to travel 200mi. If the speed of the passenger train is 25 mi/h faster than the speed of the freight train find the speed of each.
22. Ariana took 2 h longer to drive 360 mi on the first day of a trip than she took to drive 270 mi. on the second. If her speed was the same on both days, what was the driving time each day?
26. A plane flies 720 mi against a steady 30-mi/h headwind and then returns to the same point with the wind. If the entire trip takes 10 h, what is the plane’s speed in still air?
34. Kevin earned $165.00 interest for 1 year on an investment of $1500.00. At the same rate what amount of interest would be earned by an investment of $2500.00?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 18. A passenger train can travel 325 mi. in the same time a freight train takes to travel 200mi. If the speed of the passenger train is 25 mi/h faster than the speed of the freight train find the speed of each.
:
Problems states that the time for both trains is the same.
Make a time equation, T = distance/speed
:
Let s = freight speed,
(s+25) = passenger speed
:
 = = 
:
Cross multiply and you have:
325s = 200(s+25)
325s = 200s + 5000
325s - 200s = 5000
s = 5000/125
s = 40 mph freight speed, passenger speed = 65 mph
:
Check, find the times, should be equal:
325/65 = 200/40
5 = 5
:
:
:
22. Ariana took 2 h longer to drive 360 mi on the first day of a trip than she took to drive 270 mi. on the second. If her speed was the same on both days, what was the driving time each day?
:
here the speeds are equal so write a speed equation: speed = distance/time.
:
Let t = time to drive 270 mi;
(t+2) = time to drive 360 mi;
:
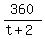 = = 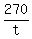
:
Cross multiply:
360t = 270(t+2)
360t = 270t + 540
360t - 270t = 540
90t = 540
t = 540/90
t = 6 hrs time to drive 270 mi, then 8 hrs to drive 360 mi
:
Check using speed, should be equal
360/8 = 270/6
45 = 45
:
:
:
26. A plane flies 720 mi against a steady 30-mi/h headwind and then returns to the same point with the wind. If the entire trip takes 10 h, what is the plane’s speed in still air?
:
Let s = speed of plane in still air
(s-30) = speed against the wind
(s+3) = speed with the wind
:
Write a time equation: time = distance/speed
:
Time against the wind + Time with the wind = 10
 + +  = 10 = 10
:
Multiply by the common denominator; (s-30)(s+30), then we have:
720(s+30) + 720(s-30) = 10(s-30)(s+30)
:
720s + 21600 + 720s - 21600 = 10(s^2 - 900)
:
1440s = 10s^2 - 9000
:
Arrange as a quadratic equation:
10s^2 - 1440s - 9000 = 0
:
Simplify, divide equation by 10
s^2 - 144s - 900 = 0
:
Factors to:
(s - 150)(s + 6) = 0
:
s = -6 (ignore this solution
and
s = + 150 mph is the planes speed in still air:
:
Check using a time equation:
720/120 + 720/180 =
6 + 4 = 10 hrs
:
:
:
34. Kevin earned $165.00 interest for 1 year on an investment of $1500.00. At the same rate what amount of interest would be earned by an investment of $2500.00?
;
Let's try using ratio, let I = interest earned at $2500:
 = = 
:
Cross multiply
1500I = 165 * 2500
I = 412500/1500
I = $275 interest earned with $2500
:
Check by finding the interest rate, should be the same:
165/1500 = 275/2500
.11 = .11
:
:
Any questions?
|
|
|