Question 723897: A motorist leaves Shellberg at 6:18 am, drives the 241 miles to Peakview , takes a 1 hour and 25 minute break and then drives a further 207 miles to Mooseville, arriving at 9:38 pm.
(a) Assuming the motorist drives at a constant speed throughout the journey, at what speed (to the nearest mile per hour) does he/she travel?
Answer: 32 miles per hour (I have this answer)
(b) If the motorist had gone 16 miles per hour faster than the speed you recorded in part (a), at what time (to the nearest minute) would he or she arrive?
Answer: pm (I know this would be 48 miles an hour.. which would be by my calculations 9 hours and 33 minutes.. when I subtract 1445 - 933 I get a difference of 5 hours and 12 minutes.. This not the right answer? Help please
(c) If the motorist had gone 20 miles per hour faster than the speed you recorded in part (a), at what time (to the nearest minute) would he or she arrive?
Answer: pm
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! (a) The time between 6:18 AM and 9:38 PM is 15 hours and 20 minutes.
In minutes, it is  minutes. minutes.
From that time we must deduct the 1 hour and 25 minutes that the motorist was not driving. (That is  minutes). minutes).
The motorist was driving for  minutes. minutes.
The distance covered was 
The speed was  which rounds to 32mph which rounds to 32mph
Answer: 32 miles per hour (you have this answer)
(b) If the motorist had gone 16 miles per hour faster than the speed you recorded in part (a), at what time (to the nearest minute) would he or she arrive?
The motorist would have been moving at 
At that speed, the motorist would have driven 448 miles in
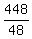 hours= hours=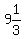 hours = 9 hours and 20 minutes = about 9.33 hours. hours = 9 hours and 20 minutes = about 9.33 hours.
That is the driving time. (It is not 9 hours and 33 minutes. I do not know why you are subtracting that time, or where you got the 1445 from).
In minutes, the driving would have taken  minutes. minutes.
Adding the same 85-minute break to the driving time, the trip would have taken
 = 10 hours and 45 minutes = 11 hours minus 15 minutes = 10 hours and 45 minutes = 11 hours minus 15 minutes
That trip time added to the 6:18 AM trip start time, would mean the trip would end at 5:03 PM. (I calculate it as 6:18 AM plus 11 hours minus 15 minutes = 5:03 PM)
Answer: 5:03 PM
(c) If the motorist had gone 20 miles per hour faster than the speed you recorded in part (a), at what time (to the nearest minute) would he or she arrive?

The time to drive 448 miles at 52 miles per hour is
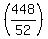 hours = hours = 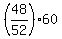 minutes = about 517 minutes (rounding to whole minutes). minutes = about 517 minutes (rounding to whole minutes).
Adding the same 85-minute break to the driving time, the trip would have taken
 = 10 hours and 2 minutes. = 10 hours and 2 minutes.
Ten hours and 2 minutes after the 6:18 AM departure would be 4:20 PM, the time for arrival at Mooseville.
Answer: 4:20 PM
|
|
|