Question 697502: kinematic question:a highway patrol at rest is passed by a bus travelling at constant speed of 126 km/h.two seconds later the patrol car starts accelerates at a constant rate of 5m/s2 until it reaches a speed of 162 km/h.if the patrol car then maintains a constant speed of 162km/h , determine the distance travelled by the patrol car to overtake the bus.
thank you tutor.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I suspect you are taking physics in high school or college.
However, to cover any possible situation, I'll add the physics "formulas" in parenthesis,
but I will show the solution as if it was a problem for a fifth grader.
A physics instructor may expect a different way to solve the problem,
but I hope I found the simplest way,
and I believe the simplest way is the best way.
Some painful conversions seem needed,
but the numbers were chosen so as to make this easier.
 m/s m/s
 m/s m/s
Accelerating from  to to  m/s at m/s at  m/s of speed increase per second takes m/s of speed increase per second takes
 seconds. seconds.
( <--> <-->  but for this case but for this case  ) )
While accelerating, the police car has an average speed of  m/s m/s
(because at constant acceleration, the average velocity is the average of the initial and final velocities)
so in  s it covers a distance of s it covers a distance of  m m
( ) )
The distance ( , in meters) covered by the bus and also by the police car can be calculated from either point of view. , in meters) covered by the bus and also by the police car can be calculated from either point of view.
( ) )
The bus is moving for  seconds at seconds at  m/s, covering a distance of m/s, covering a distance of
 meters. meters.
During those  seconds, the police car is stopped for 2 seconds, seconds, the police car is stopped for 2 seconds,
covers 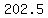 m for the next m for the next  seconds (while accelerating), seconds (while accelerating),
and after those first  seconds, seconds,
moves at  m/s for the rest of the time ( m/s for the rest of the time ( seconds). seconds).
The distance covered by the police car is
 meters meters
Because the same distance  is covered by the bus and by the car is covered by the bus and by the car
during the  seconds between the time the bus passes the patrol car and the time the patrol car overtakes the bus. seconds between the time the bus passes the patrol car and the time the patrol car overtakes the bus.
 --> -->  --> -->  --> -->  --> -->  seconds. seconds.
Substituting into  we get we get
 --> -->  meters (about 1 km). meters (about 1 km).
|
|
|