Question 669082: In a 100-meter race, Todd crosses the finish line 5 meters ahead of Scott. To even things up, Todd suggests to Scott that they race again, this time with Todd lining up 5 meters behind the start.
(a) Assuming that Todd and Scott run at the same pace as before, does the second race end in a tie?
(b) If not, who wins?
(c) By how many meters does he win?
(d) How far back should Todd start so that the race ends in a tie?
After running the race a second time, Scott, to even things up, suggests to Todd that he (Scott) line up 5 meters in front of the start.
(e) Assuming again that they run at the same pace as in the first race, does the third race result in a tie?
(f) If not, who wins?
(g) By how many meters?
(h) How far ahead should Scott start so that the race ends in a tie?
I understand that Scott is running at 0.95 times the speed of Todd but that's all I understand. I think that I could do the second half after seeing and understand how the first half is done. Thanks so much!
Found 2 solutions by ankor@dixie-net.com, MathTherapy:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a 100-meter race, Todd crosses the finish line 5 meters ahead of Scott. To even things up, Todd suggests to Scott that they race again, this time with Todd lining up 5 meters behind the start.
:
Assume that Todd runs it in 10 sec
100/10 = 10 m/sec is Todd's running speed
then
95/10 = 9.5 m/sec is Scott's speed
:
(a) Assuming that Todd and Scott run at the same pace as before, does the second race end in a tie?
Find Todd's time to run 105 meters: 105/10 = 10.5 sec
Find Scott's time to run 100 meters: 100/9.5 = 10.5263 sec
:
(b) If not, who wins?
Todd still wins, but Scott is only .0263 sec behind him
:
(c) By how many meters does he win?
.0263 * 9.5 ~ .25 meters
(d) How far back should Todd start so that the race ends in a tie?
let a = distance back for Todd so it end's in a tie, write a time equation
 = = 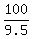
cross multiply
9.5(a+100) = 10*100
9.5a + 950 = 1000
9.5a = 1000 - 950
9.5a = 50
a = 50/9.5
a = 5.263 meters behind
:
After running the race a second time, Scott, to even things up, suggests to Todd that he (Scott) line up 5 meters in front of the start.
(e) Assuming again that they run at the same pace as in the first race, does the third race result in a tie?
We know Todds time to run 100 m = 10 sec
Find Scotts time to run 95 m: 95/9.5 = 10 sec
:
(f) If not, who wins?
A tie
:
(g) By how many meters?
(h) How far ahead should Scott start so that the race ends in a tie?
I understand that Scott is running at 0.95 times the speed of Todd but that's all I understand. I think that I could do the second half after seeing and understand how the first half is done. Thanks so much!
0 solutions
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In a 100-meter race, Todd crosses the finish line 5 meters ahead of Scott. To even things up, Todd suggests to Scott that they race again, this time with Todd lining up 5 meters behind the start.
(a) Assuming that Todd and Scott run at the same pace as before, does the second race end in a tie?
(b) If not, who wins?
(c) By how many meters does he win?
(d) How far back should Todd start so that the race ends in a tie?
After running the race a second time, Scott, to even things up, suggests to Todd that he (Scott) line up 5 meters in front of the start.
(e) Assuming again that they run at the same pace as in the first race, does the third race result in a tie?
(f) If not, who wins?
(g) By how many meters?
(h) How far ahead should Scott start so that the race ends in a tie?
I understand that Scott is running at 0.95 times the speed of Todd but that's all I understand. I think that I could do the second half after seeing and understand how the first half is done. Thanks so much!
Let Todd’s speed be S
Since Todd finishes the 100-meter race 5 meters ahead of Scott, then Todd’s time to run 100 m = 100/S
Since Todd finished 5 m ahead of Scott, then Scott completed 95 (100 – 5) m in the same time 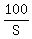 that Todd completed the 100 m trip. Therefore, Scott’s speed = that Todd completed the 100 m trip. Therefore, Scott’s speed = 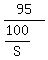 , or , or  m/s m/s
For the 2nd race, Todd’s distance will be 105 (5 + 100) m
Therefore, time that Todd will take to complete 105 m = 
For the 2nd race, Scott’s distance will be 100 m
Therefore, time that Scott will take to complete 100 m = 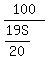 , or , or  seconds seconds
Todd’s time: 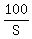 ----- -----  ----- Multiplying by 19 to make denominator, 19S ----- Multiplying by 19 to make denominator, 19S
Scott’s time = 
a)______As seen above, the race DOESN’T end in a tie.
b)______Todd would still win since his time is shorter than Scott’s ( , compared to , compared to  ) )
c)______Since Todd will win, he would’ve completed 105 m. However, Scott will cover  , or 99.75 m, so Todd wins by a , or 99.75 m, so Todd wins by a  -meter margin -meter margin
d)______For the race to end up in a tie, then both have to finish at the same time. Therefore, with Todd's distance being 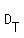 , and Scott's distance, , and Scott's distance, 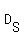 , we get: , we get:  , or , or  , which signifies that , which signifies that  , and , and  , and that Todd needs to start at the starting point ( , and that Todd needs to start at the starting point ( m starting point), while Scott needs to start 5 m ahead, or at the + m starting point), while Scott needs to start 5 m ahead, or at the + m mark m mark
e)______As pointed out in d), Scott being 5 m ahead of the starting point will tie Todd. This is confirmed as Todd’s time to run 100 m, equals Scott’s time to run 95 m, based on their constant speeds, or,  , ,  , or 1,900S = 1,900S , or 1,900S = 1,900S
f)______No one wins, as discussed/shown in e)
g)______N/A
h)______N/A
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|