Question 581527: The train from C to D breaks down after 1 hour. The train has stopped because of 1/2 hour repairs, then, it continues on at 3/4 of its beginning rate, arriving at B 2 hours late. If the train had covered 75 miles more before the break down, it could be only1 hour late. What is the beginning rate of the train? Explain how you would get the answer.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The train from C to D breaks down after 1 hour.
The train has stopped because of 1/2 hour repairs, then, it continues on at 3/4 of its beginning rate, arriving at B 2 hours late.
If the train had covered 75 miles more before the break down, it could be only 1 hour late.
What is the beginning rate of the train? Explain how you would get the answer.
:
Let s = original speed of the train, also distance traveled in 1 hr
then
.75s = speed after the breakdown
:
let d = distance from C to D
then
 the normal time for the trip the normal time for the trip
Distance traveled to the breakdown: 1 * s = s miles
(d-s) = distance traveled at .75s
and
 = time at slower rate = time at slower rate
write a time equation
1 + .5 +  = =  + 2 + 2
1.5 +  = =  + 2 + 2
 = =  + 2 - 1.5 + 2 - 1.5
 = =  + .5 + .5
multiply by .75s to clear the denominators
d - s = .75d + .5(.75s)
d - s = .75d + .375s
d - .75d = .375s + s
.25d = 1.375s
multiply both sides by 4
d = 5.5s
:
"If the train had covered 75 miles more before the break down, it could be only 1 hour late."
I made a big mistake here, instead "75 mi more" I used 75 mi, try to correct this now
:
write a time equation,
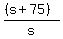 + .5 + + .5 + 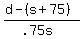 = =  + 1 + 1
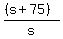 + + 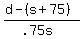 = =  + 1 - .5 + 1 - .5
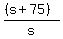 + + 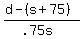 = =  + .5 + .5
Multiply by .75s to clear the denominators
.75(s+75) + (d-s-75) = .75d + .5(.75s)
.75s + 56.25 + d - s - 75 = .75d = .375s
Combine like terms
.75s - s - .375s + d - .75d = 75 - 56.25
-.625s + .25d = 18.75
Replace d with 5.5s
-.625s + .25(5.5s) = 18.75
-.625s + 1.375s = 18.75
.75s = 18.75
s = 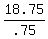
s = 25 mph is the initial speed of the train
:
:
See if this checks out, d = 5.5(25) = 137.5 mi and .75(25) = 18.75 mph
 + .5 + + .5 + 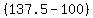 = = 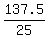 + 1 + 1
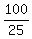 + + 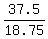 = = 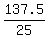 + .5 + .5
4 + 2 = 5.5 + .5; checks out
|
|
|