Question 426400: It takes a freight train 3 hours more to travel 280 miles than it takes an express train to travel 200 miles. The rate of the express is 10 miles per hour faster the the rate of the freight train. Fine the rates of both trains.
Found 3 solutions by mananth, ikleyn, josgarithmetic:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! Freight train x mph 280 miles
Express train x +10 mph 200 miles
t=d/r
280/x=200/(x+10)+3
280/x-200 /(x+10)=3
LCD = x(x+10)
Multiply by LCD
280(x+10)-200x=3x(x+10)
280x+2800-200*x =3x^2+30
3X^2+80x-2770=0
Find the roots of the equation by quadratic formula
a=3 b=80 c=-2770
b^2-4ac=6400+33240
b^2-4ac=39640
x1=(-80 +199.1)/6
x1=19.85
x2=(-80 -199.1)/6
x2= -46.52
Ignore negative value
x=19.85 mph Freight train speed
29.85 mph=Express train speed
Answer by ikleyn(53427)  (Show Source):
You can put this solution on YOUR website! .
It takes a freight train 3 hours more to travel 280 miles than it takes an express train to travel 200 miles.
The rate of the express is 10 miles per hour faster the rate of the freight train. Fine the rates of both trains.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @mananth is incorrect - it has fatal arithmetical errors.
I came to bring a correct solution.
Freight train speed x mph, distance 280 mile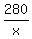s, travel time is  hours.
Express train speed (x+10) mph, distance 200 miles, travel time is 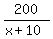 hours.
Time equation
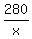=  + 3. (1)
Multiply all the terms by x(x+10)
280(x+10) = 200x + 3x*(x+10).
Reduce to the standard form quadratic equation
280x + 2800 = 200x + 3x^2 + 30x
3x^2 - 50x - 2800 = 0.
Use the quadratic formula and find the roots.
To avoid mechanical calculations, I used the online solver
https://www.calculatorsoup.com/calculators/algebra/quadratic-formula-calculator.php/
It produced two roots - one was positive, the other was negative.
I rejected the negative root and accepted the positive one, which was 40.
So, the freight train speed was 40 mph, while the express train speed w3as 40+10 = 50 mph. <<<---=== ANSWER
CHECK equation (1).
Its left side is  = 7.
Its right side is 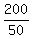 + 3 = 7.
Both values coincide - hence, the solution is correct.
Solved correctly.
Answer by josgarithmetic(39702)  (Show Source):
You can put this solution on YOUR website!
SPEED TIME DISTANCE
Freight r 280/r 280
Express r+10 200/(r+10) 200
DIFFERENCE 3
 Solve this for r.
Start by multiply both sides by  .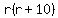
.
.
|
|
|
