Question 389977: At 6:00 am, the Eilerman family left for Christmas vacation and drove south at an average speed of 40 mph. Their friends, the Knapke's, left two hours later and traveled the same route at an average speed of 55 mph. At what time could the Knapke's expect to overtake the Eilerman's?
Okay, so I know the Knapke's started at 8:00 am. After that, I'm lost. Please help.
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! At 6:00 am, the Eilerman family left for Christmas vacation and drove south
at an average speed of 40 mph.
Their friends, the Knapke's, left two hours later and traveled the same route
at an average speed of 55 mph.
At what time could the Knapke's expect to overtake the Eilerman's?
:
Let t = K family's travel time
then
(t+2) = E family's travel time
:
When K overtakes E, they will have traveled the same distance
Write a dist equation: dist = speed * time
:
K's dist = E's dist
55t = 40(t+2)
55t = 40t + 80
55t - 40t = 80
15t = 80
t =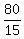 
t = 5 hrs or 5 hrs 20 min; K's travel time
:
K started at 8:00 AM therefore, they will catch E at 1:20 PM
:
:
Check solution by finding the distances
55 * 5.33 = 293.33 mi
40 * 7.33 = 293.33 mi
|
|
|
