Question 389640: Ok...I think I might be confusing myself (lol)...so I just want to check this out with you all...
"An airplane is traveling due west at 1240ft/sec and Santa's sleigh is traveling due east at 5450ft/sec...
A. If Rudolf can spot airplanes 10,000ft ahead of him and Santa's sleigh and an airplane are 25,000ft away from each other, how many seconds will it take Rudolf to spot the airplane?"
I'm not sure if I need to add both rates together and then divide the distance (either 25,000ft...10,000ft ...or 15,000ft (25,000-10,000ft)) by both rates and then figure out the time that way...?
And...
B. If Santa's sleigh needs 2500ft to turn out of the way of another aircraft, how long does Rudolf have to inform Santa and turn the sleigh if he spots the aircraft when it is 10,000ft away?
Same problem...I'm not sure if I'm setting up this problem right...
Is it 10,000-2500= 7500/(5450+1240)=1.12 sec...?
Thanks for your help! *smiles*
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x = number of seconds that the sleigh and airplane have been traveling
In this case, a picture is worth a thousand words (and symbols). So let's draw one

In the picture above, we can see that Santa has traveled 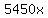 feet (first segment shown in red). Recall that feet (first segment shown in red). Recall that  (distance = rate*time). In this case, the rate is 5450ft/sec, so r=5450 and he has been traveling for 'x' seconds. So t=x (distance = rate*time). In this case, the rate is 5450ft/sec, so r=5450 and he has been traveling for 'x' seconds. So t=x
Likewise, the airplane has been traveling at a speed of 1240 ft/sec for 'x' seconds as well. So it has traveled 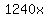 ft (last segment shown in red). ft (last segment shown in red).
The final middle segment has a length of 10,000 ft. because we want the distance between the two to be 10,000 ft at t = x seconds.
Since the entire distance between them is 25,000 ft, this means that the length of the entire red line is 25,000 ft. So the individual pieces must add to 25000.
So this means that  . .
Let's solve for 'x' to find the time it will take for Rudolf to spot the airplane.
 Start with the given equation. Start with the given equation.
 Combine like terms on the left side. Combine like terms on the left side.
 Subtract Subtract 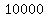 from both sides. from both sides.
 Combine like terms on the right side. Combine like terms on the right side.
 Divide both sides by Divide both sides by 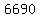 to isolate to isolate  . .
 Reduce. Reduce.
 Use a calculator to find the decimal approximation Use a calculator to find the decimal approximation
So at approximately 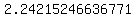 seconds, the sleigh and the airplane will be 10,000 ft apart. seconds, the sleigh and the airplane will be 10,000 ft apart.
So it will take about 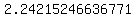 seconds for Rudolf to spot the airplane. seconds for Rudolf to spot the airplane.
-------------------------------------------------------------
b) I'll let you try this part on your own. I recommend using the picture above as a guide.
Hint: Since the sleigh needs 2500 ft of clearance, the distance between the plane and the sleigh has been reduced to 2500 ft (instead of 10,000). Once you find this new value of t, subtract it from the answer in part a) to find the elapsed time window that Rudolf has (ie the window for his reaction). If you're still stuck, let me know.
If you need more help, email me at jim_thompson5910@hotmail.com
Also, feel free to check out my tutoring website
Jim
|
|
|