Question 356735: A mother horse and a baby horse walk 10 miles from point A to point B. The motherís speed is 10 miles per hour and the babyís 5 miles per hour. The mother rests for 2 minutes after every x minutes of walking. The baby keeps walking. They arrive together at the destination. Find the range of x.
Found 2 solutions by ankor@dixie-net.com, onlinepsa:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A mother horse and a baby horse walk 10 miles from point A to point B.
The motherís speed is 10 miles per hour and the babyís 5 miles per hour.
The mother rests for 2 minutes after every x minutes of walking.
The baby keeps walking. They arrive together at the destination.
Find the range of x.
:
Find the time it takes to go from A to B, using the baby's speed
 = 2 hrs = 2 hrs
:
Find the actual walking time of Mama
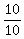 = 1 hr = 1 hr
then
Mama spends a total of 1 hr not walking
Not walking time = walking time
therefore
After two min of walking (x), she rests two minutes
x = 2
Answer by onlinepsa(22)   (Show Source): (Show Source):
You can put this solution on YOUR website! The baby horse's speed is 5 miles per hour; thus it will take 2 hours to cover a distance of 10 miles from A to B.
The mother horse's speed is 10 miles per hour; if she does not stop anywhere she should take 1 hr to reach B. But she arrives at B at the same time as the baby. Thus, she spends 1 hr of time resting.
In an ideal situation, if she spends 2 minutes for each 'break' she would have taken 30 breaks. Thus, the one hour of walking when divided by '30' should give us x=2. Or, she does a 2 minutes of walk and then rests for 2 minutes.
However, the above is NOT correct. [No doubt author's question is 'range of x' and NOT 'value of x']
Her walking & resting forms the pattern - W, R, W, R, W , R ....
Think about the answer to the question - What does she do at last- 'W' [for walking] or 'R' [for resting]? Invariably our above method says, she already reached B and then rested for '2 minutes' at B after which the baby arrives. This violates "They arrive together at the destination".
We must notice that the number of breaks will be one less than total number of 'walks'; the last should be 'W' when she reaches B.
[As in W, R, W or W, R, W, R, W and so on].
Let the number of 'walks' be 'b' where each 'walk' is of 'x' minutes; therefore, the number of breaks [of 2 minutes] will be b-1.
According to the question,
b*x+ (b-1)*2=120
bx + 2b= 122
x=(122/b)-2
As, we already said, number of breaks cannot be 30 or x cannot be ideally equal to '2'. It must be less than 2. Also it must be greater than 0.
Thus, range of x is: 2>x>0.
[Since, 'b' is an integral value we can also find out the exact number of values of x here.
2>x>0
=>2>(122/b)-2>0
=>4>(122/b)> 2
=>61> b> 30.5
b ranges from 31 to 60; there are 30 unique values of x possible.]
Hope this helps!
Thanks,
PRD
https://onlinepsa.wordpress.com
|
|
|