SOLUTION: Below are two questions that I was able to see the answer for in the answer key, but have no idea how they arrived at the answer. can you please explain? Two cyclists start bik

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: Below are two questions that I was able to see the answer for in the answer key, but have no idea how they arrived at the answer. can you please explain? Two cyclists start bik      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 202965: Below are two questions that I was able to see the answer for in the answer key, but have no idea how they arrived at the answer. can you please explain?
Two cyclists start biking from a trail's start 3 hours apart. The second cyclist travels at 10 miles per hour and starts 3 hours after the first cyclist who is traveling at 6 miles per hour. How much time will pass before the second cyclist catches up with the first from the time the second cyclist started biking?
A. 2 hours
B. 4 ½ hours
C. 5 ¾ hours
D. 6 hours
E. 7 ½ hours
. Jim can fill a pool carrying buckets of water in 30 minutes. Sue can do the same job in 45 minutes. Tony can do the same job in 1 ½ hours. How quickly can all three fill the pool together?
A. 12 minutes
B. 15 minutes
C. 21 minutes
D. 23 minutes
E. 28 minutes



Found 3 solutions by solver91311, Edwin McCravy, Earlsdon:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!

In 3 hours, the first guy is 3 times 6 = 18 miles ahead. If he then stopped and the 2nd guy went 4mph (10 - 6), how long would it take him to go 18 miles?

*************************************************************

If A can do a job in x time periods, then A can do of the job in 1 time period. Likewise, if B can do the same job in y time periods, then B can do of the job in 1 time period, and so on...

So, working together, they can do



of the job in 1 time period.

Therefore, they can do the whole job in:



time periods.



John

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Edwin's solution:
Below are two questions that I was able to see the answer for in the answer key, but have no idea how they arrived at the answer. can you please explain?
Two cyclists start biking from a trail's start 3 hours apart. The second cyclist travels at 10 miles per hour and starts 3 hours after the first cyclist who is traveling at 6 miles per hour. How much time will pass before the second cyclist catches up with the first from the time the second cyclist started biking?
A. 2 hours
B. 4 ½ hours
C. 5 ¾ hours
D. 6 hours
E. 7 ½ hours 

The cyclist who started first had gone 3 hours at 6 mph,
and therefore had an 18 mile head start when the second 
cyclist started.  The second cyclist travels at 6 mph, 
and so his (or her) approach rate to the first cyclist 
is the difference in their speeds or 10-6 or 4mph.  So 
the 18 mile distance between them shrinks at the rate 
of 4mph. Since time = distance/rate

t+=+18%2F4+=+9%2F2+=+4%261%2F2 hours. So the correct answer is B.

-------------------------------

Jim can fill a pool carrying buckets of water in 30 minutes.
Sue can do the same job in 45 minutes. Tony can do the same
job in 1 ½ hours. How quickly can all three fill the pool
together?
A. 12 minutes
B. 15 minutes
C. 21 minutes
D. 23 minutes
E. 28 minutes 

1%261%2F2 hours = 90 minutes. 
The least common multiple of 30 minutes, 45 minutes and 90 minutes,
is 90 minutes.

In 90 minutes Jim can fill 3 pools, Sue can fill 2 pools, and Tony
can fill 1 pool.  So working together they can fill 3+2+1 or 6 pools 
in 90 minutes, so their combined rate is %286_pools%29%2F%2890_minutes%29
which reduces to %281_pool%29%2F%2815_minutes%29 so it will take them 15
minutes to fill 1 pool.

So the correct answer for this one is also B.

Edwin

Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Problem 1. )d = distance, r = rate(speed), and t = time of travel)
For the first cyclist:
d%5B1%5D+=+r%5B1%5D%2At%5B1%5D
For the second cyclist:
d%5B2%5D+=+r%5B2%5D%2At%5B2%5D
The question is at what time, t, will d%5B1%5D+=+d%5B2%5D?
The first cyclist travels 3 hours longer than the second cyclist, so...
t%5B1%5D+=+t%5B2%5D%2B3, so rewriting the first two equations, we get:
d%5B1%5D+=+6%28t%5B2%5D%2B3%29 and
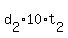d%5B2%5D++10%2At%5B2%5D but, when the cyclists meet, d%5B1%5D+=+d%5B2%5D, so...
6%28t%5B2%5D%2B3%29+=+10%2At%5B2%5D Solve for t%5B2%5D.
6%2At%5B2%5D%2B18+=+10%2At%5B2%5D Subtract 6%2At%5B2%5D from both sides.
18+=+4%2At%5B2%5D Divide both sides by 4.
t%5B2%5D+=+4.5hours.
The second cyclist will catch up with first cyclist after 4.5 hours.
The first cyclist however will have traveled for (4.5+3) = 7.5 hours.
So if you start counting when the first cyclist begins, then the answer is 7.5 hours.
If you start counting when the second cyclist begins, then the answer is 4.5 hours.
The problem is not clear as to when you should start the clock!
Problem 2.
It's best to work out the rate (per minute) at which each of the three individuals work.
If Jim can fill the pool in 30 minutes, then he can fill 1/30 of the pool in 1 minute.
If Sue can fill the pool in 45 minutes, then she can fill 1/45 of the pool in 1 minute.
If Tony can fill the pool in 1 1/2 hours (that's 90 minutes), then he can fill 1/90 of the pool in 1 minute.
Working together, the three of them can fill (1/30 + 1/45 + 1/90 = 1/15) of the pool in 1 minute.
This means that they can fill the entire pool in 15 minutes working together.