Question 201710: If a race car can go around a track in 5 minutes,then how long will it take to go around the track if it increases its speed by 20%?
Found 4 solutions by RAY100, Theo, ikleyn, greenestamps:
Answer by RAY100(1637)   (Show Source): (Show Source):
You can put this solution on YOUR website! v=d/t
.
(1) v=d/5
.
(2) 1.2 v = d/t
.
from (2),,v=d/(1.2 t) = d /5,,,,,,from(1)
.
1.2 t =5
.
t= 5/1.2 = 4.17 min
.
checking,,,,let d=10, v= 10/5 =2
v2= 10/4.17 = 2.4
.
2.4 / 2 = 1.2,,,or 20 % higher,,,ok
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the answer should be 5/1.2 = 4.16666666 minutes = 4 minutes and 10 seconds.
here's how I got it.
basic formula is rate * time = distance.
D is going to be the same so we call it D.
The rate will be different so we'll call it R1 and R2.
the time will be different so we'll call it T1 and T2.
we know the following:
R1 * T1 = D
T1 = 5, so
R1 * 5 = D
we know that R2 will be 20% more than R1 so we know that R2 = 1.2 * R1.
we can make a general equation for R2 that says
R2 * T2 = D
R2 will be different.
T2 will be different.
D will remain the same.
since we know that R2 = 1.2 * R1, we can substitute to get
1.2 * R1 * T2 = D
since they both = D, we can make them equal to each other, so we have
R1 * T1 = 1.2 * R1 * T2
since we know that T1 = 5, we can substitute in the equation to get
R1 * 5 = 1.2 * R1 * T2
if we divide both sides of the equation by 1.2 * R1, then we get
5/1.2 = T2
simplifying gets 4.16666666 = T2
taking the fraction and converting it to minutes we get
.1666666666 * 60 = 10
which gets us
4 minutes and 10 seconds.
to check this out, we make an assumption by saying the distance is an arbitrary number such as 10 miles.
In order for this to be done in 5 minutes, the car has to go 10 / 5 minutes = 2 miles a minute which equates to 120 miles an hour.
if we raise 2 miles a minute by 20% we get 2.4 miles a minute which equates to 144 miles an hour.
at 2.4 miles a minute, it takes 10 / 2.4 minutes to complete the distance which equals 4.166666666 minutes which gets us to our answer so we're good.
Answer by ikleyn(52958)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If a race car can go around a track in 5 minutes, then how long will it take to go around the track
if it increases its speed by 20%?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is simple - so, the solution must be simple and short.
Let 'd' be the circumference (the length from start to finish). It is not given in the problem.
Let 'v' be the average speed of the car.
We are given that the travel time is 5 minutes. It means
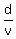 = 5 minutes.
Now 'v' increases by 20%. The new speed is now 1.2v, and they want you evaluate = 5 minutes.
Now 'v' increases by 20%. The new speed is now 1.2v, and they want you evaluate 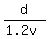 .
We write .
We write
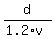 = = 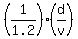 = we replace here = we replace here 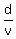 by 5 and continue =
= by 5 and continue =
= 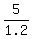 = 4.16161616... minutes (infinite periodical decimal fraction)
So, the answer is 4.16161616... minutes.
5 minutes is the same as 5*60 = 300 seconds, so, in seconds, the new travel time is = 4.16161616... minutes (infinite periodical decimal fraction)
So, the answer is 4.16161616... minutes.
5 minutes is the same as 5*60 = 300 seconds, so, in seconds, the new travel time is
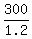 = 250 seconds, or 4 minutes and 10 seconds. = 250 seconds, or 4 minutes and 10 seconds.
Thus the problem is solved completely, with explanations accessible to a beginner student.
I showed you a formal way to solve, but much shorter than @Theo's explanations in his post.
============================================
Another way reasoning is THIS:
The speed increased in 1.2 times, the distance remained the same - - - hence, the time decreased in 1.2 times.
So, the new time is 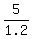 minutes = 4.16161616... minutes = 4 minutes and 10 seconds. minutes = 4.16161616... minutes = 4 minutes and 10 seconds.
Thus, you have two ways to build your solution: one way is formal, another way is informal and short.
You should understand both ways. They both are elementary.
Answer by greenestamps(13219)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the distance is the same and the speed increases by a factor of 120/100 = 6/5, then the time required is decreased by a factor of 6/5 -- i.e. multiplied by a factor of 5/6.
(5 minutes) * (5/6) = 25/6 minutes = 4 1/6 minutes = 4 minutes 10 seconds
ANSWER: 4 minutes and 10 seconds
|
|
|