Question 125482: Either I missed something or the plane has lost distance.
A plane climbs into the jet stream which is flowing at a rate of 80 miles per hour. It travels with the jet stream for 5 hours and then reduces its altitude, flying out of the jet stream for 4 more hours. The plane, while out of the jet stream, covered 550 miles less than it did during the 5 hours it was in the jet stream. How fast was the plane flying out of the jet stream?
Found 2 solutions by solver91311, josmiceli:
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! Use the distance = rate times time formula, 
Since we are trying to find the rate for the plane out of the jet stream, let that rate be r. Then we know that the rate while in the jet stream must be r + 80.
The distance traveled while in the jet stream, d, must be equal to the rate while in the jet stream times the 5 hours that it flew in the jet stream, or:
The distance traveled while out of the jet stream is 550 miles less than the distance traveled in the jet stream, so we can express that distance as 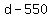 , but we can also express this distance as r, the rate out of the jet stream times 4, the number of hours flown out of the jet stream, or:
Re-writing the first equation we get:  , giving us an expression for d that can be substituted into the second equation:
 , the speed of the aircraft out of the jet stream.
Check the answer.
If the speed out of the jet stream is 150, then the speed in the jet stream must be 230. 230 times 5 = 1150, so the airplane traveled 1150 miles while in the jet stream.
The speed out of the jet stream is 150, so the distance traveled out of the jet stream is 150 times 4 = 600, and 600 = 1150 - 550. Answer checks.
Answer by josmiceli(19441)  (Show Source):
|
|
|
