SOLUTION: Modern oil tankers weigh over a half-million tons and have lengths of up to one-fourth mile. Such massive ships require a distance of 4.3 km (about 2.7 mi) and a time of 16 min to

(a)  This motion is uniform deceleration with constant deceleration.

     Let "a" be the value of the constant deceleration.


     From Physics (Mechanics and Kinematics), having given the initial speed of 32 km/h
     and time 16 minutes to stop, we can calculate the average deceleration

         a = 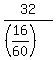 =  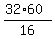= 2*60 = 120 km/h^2.


     Here the ratio 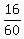 is the time of 16 minutes converted to hours.

     Converted to m/s^2, this value of 120 km/h^2 is  

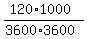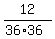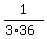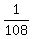          =  =  =  m/s^2 = 0.00926 m/s^2  (rounded).

     This value  0.00926 m/s^2 is the answer (average deceleration in m/s^2) for part (a).



(b)  The speed is linear function of time in this motion.

     The maximum value of the speed is 32 km/h; the minimum value is 0 km/h, when the ship stops.

     The magnitude of the ship's average velocity in km/h is 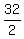  = 16 km/h,

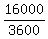     or   m/s =  m/s = 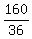 =  m/s = 4 m/s = 4.44444 m/s (rounded).

     This value  4 = 4.44444 m/s is the answer (ship's average speed in m/s) for part (b).