Question 1204876: A race car starts from rest and travels east along a straight and level track. For the first 5.0 s of the car's motion, the eastward component of the car's velocity is given by vx(t) = (0.860 m/s^3)t^2. What is the acceleration of the car when vx = 12.0vm/s?
problem from Young and Freedman. University Physics with Modern Physics. Fifteenth Edition.
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A race car starts from rest and travels east along a straight and level track.
For the first 5.0 s of the car's motion, the eastward component of the car's velocity
is given by vx(t) = (0.860 m/s^3)t^2. What is the acceleration of the car when vx = 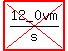 12.0 m/s ? 12.0 m/s ?
problem from Young and Freedman. University Physics with Modern Physics. Fifteenth Edition.
~~~~~~~~~~~~~~~~~~~~~~
(1) In your post, I fixed errors where I saw them. Instead of 12.0vm/s should be 12.0 m/s.
(2) Everythere in the formulas, where you see lowercase letter x, it is, actually, subscript x.
It only designates x-component of the velocity.
It is strange that in this problem they abused writing x everywhere.
It easily could be omitted, at all, since y-component ABSENTS in this problem.
Solution
For x-component of the car's velocity we have this expression
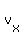 (t) = (t) = 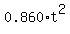 (1) (given)
(distance in meters, time in seconds). Notice that this movement is neither uniform nor uniformly accelerated.
It is a movement with variable acceleration.
The acceleration of the car a(t) is the derivative of the speed function of time.
So we write accordingly
dv(t) (1) (given)
(distance in meters, time in seconds). Notice that this movement is neither uniform nor uniformly accelerated.
It is a movement with variable acceleration.
The acceleration of the car a(t) is the derivative of the speed function of time.
So we write accordingly
dv(t)
 = -------, or a(t) = (0.860*t^2)' = 2*0.860*t = 1.720*t. (2)
dt
Next, we want to know at which time t = -------, or a(t) = (0.860*t^2)' = 2*0.860*t = 1.720*t. (2)
dt
Next, we want to know at which time t 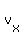 (t) = 12.0 m/s.
Using expression (1) for (t) = 12.0 m/s.
Using expression (1) for 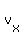 (t), we write (t), we write
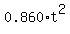 = 12, = 12,  = = 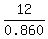 = 13.95348837, t = = 13.95348837, t = 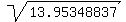 = 3.73544 s (rounded).
Notice that this time t = 3.73544 seconds is less than 5 seconds; so, according to the problem, all the formulas,
which we used on the way, were valid.
Now we make the final step: to learn what is the acceleration of the car at the time moment 3.73544 seconds,
we simply substitute t= 3.73544 into the formula (2) for acceleration, which we derived earlier.
It gives us a(3.73544) = 1.720*3.73544 = 6.4249568 m/s^2.
You may round it in a way you need / (you want).
At this point, all separate pieces are connected together, and we have the
ANSWER. When = 3.73544 s (rounded).
Notice that this time t = 3.73544 seconds is less than 5 seconds; so, according to the problem, all the formulas,
which we used on the way, were valid.
Now we make the final step: to learn what is the acceleration of the car at the time moment 3.73544 seconds,
we simply substitute t= 3.73544 into the formula (2) for acceleration, which we derived earlier.
It gives us a(3.73544) = 1.720*3.73544 = 6.4249568 m/s^2.
You may round it in a way you need / (you want).
At this point, all separate pieces are connected together, and we have the
ANSWER. When 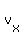 = 12.0 m/s, the acceleration of the car is 6.4249568 m/s^2. = 12.0 m/s, the acceleration of the car is 6.4249568 m/s^2.
Solved.
------------------
It is not an easy task to understand this interweaving and interaction of concepts and numbers.
To do this, you need to firmly know their meaning, definitions and interconnections.
Also, knowledge of Calculus is a MUST.
I hope that my post will help you to navigate in this ocean.
|
|
|