Question 1203680: On a planet, a rock is dropped from the top of a 400-foot cliff. After 1 second, the rock is traveling 28 feet per second. After 5 seconds, the rock is traveling 140 feet per second
a. Assume that the relationship between time, t, and speed, s, is linear and write an equation describing this relationship. Use ordered pairs of the form (time, speed).
b. Use this equation to determine the speed of the rock 6 seconds after it was dropped.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52914)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The answer to question (b) in the post by @MathLover1 is incorrect.
Below I explain WHY.
The matter is that question (b) is a TRAP.
In this problem, the acceleration of the free fall (= the gravity acceleration) of this planet is 28 ft/s^2.
Anyone who knows the beginning of Kinematics, can easily calculate that the distance
covered by the free falling body at such acceleration in 6 seconds is
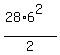 = 504 ft, = 504 ft,
which is greater than 400 ft, the height of the cliff.
So, at the time t= 6 seconds, this rock will be at the base of the cliff
and its speed will be, presumably, 0 (zero) ft/s.
|
|
|