SOLUTION: A train traveling from Avondale to Bimmaeus stops at a cracked rail after 1 hour, and the engineer spends half an hour fixing it. After which it proceeds at four fifths its usual r

Let D be the entire distance from A to B (in miles),
and let d be the distance from A to the incident point X.
Let "u" be the regular speed of the train, in miles per hour.


The train moved from A to X with its usual speed "u".
The time is 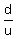   hours.


Then the train moved from X to B with the speed of 0.8u.
The time is    hours.


The total moving time is   +   hours in this scenario.


The REGULAR total moving time is 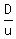   hours, and we are given that 

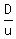     +  -  = 2 - 0.5 = 1.5  hours.              (1)


        Notice that the moving time, ONLY, is in both sides of equation (1).



In the second scenario, everything is similar, but we should replace d 
in equation (1) by (d+80). We have then the second equation in the form

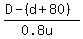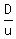     +  -  = 1 - 0.5 = 0.5  hours.    (2)


        Notice that the moving time, ONLY, is in both sides of equation (2).



Now subtract equation (2) from equation (1).  You will get

     +  = 1.    (3)


    +------------------------------------------------------------+
    |    Thus we get this simple equation (3) for the unknown    |
    |    quantity u, which is under the problem's question.      |
    +------------------------------------------------------------+


Simplify this equation (3) and find "u"


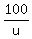     +  = 1

     = 1

    u = 20.


ANSWER.  The regular speed of the train is 20 miles per hour.

 
Ikleyn's solution is CORRECT.  I overlooked the word "MORE", and solved this
problem instead, where the "....." is below.  It is a much harder problem that
way.

Here is the more difficult solution to the problem without the word "MORE": 

 

The above drawing represents the two situations.

x = distance from A to cracked rail
y = distance from cracked rail to B
z = distance from cracked rail to B if cracked rail were 80 miles from A.

Let r = the usual speed of the train
Let h = the number of hours the train would take to go from A to B at 
the usual speed r.  So using d=rt, we have AB = hr. From that and the 
drawing above, we have:

(1)  Distance AB = x+y = 80+z = hr

Make this DRT chart for the 4 distances in
the drawings above:

Distance | Rate | time
    x    |  r   |  1
    y    | 4/5r | (h+2)-(1)-(1/2) = h+1/2
   80    |  r   | 80/r
    z    | 4/5r | (h+1)-(80/r)-(1/2) = h-80/r+1/2

I will explain the times for distances y and z.

Time for traveling the y miles:
The train was 2 hours late, so it arrived in h+2 hours
after leaving A. However, 1 hour was spent traveling 
the x miles, and another 1/2 hour was spent fixing the 
cracked rail.  So we cannot count those times for the 
time traveling the y miles. So we must subtract those 
times from the total h+2 hours. Thus the time for 
traveling the y miles is
(h+2)-(1)-(1/2) = h+1/2

Time for traveling the z miles:
The train would have been 1 hour late, so it would have 
arrived in h+1 hours after leaving A.  However, using 
t=d/r, 80/r hours would have been spent traveling the 
80 miles, and 1/2 hour would have been spent fixing the 
cracked rail.  So we cannot count those times 
for the time traveling the z miles. So we must subtract 
those times from the total h+1 hours.  Thus the time for 
traveling the z miles is
(h+1)-(80/r)-(1/2) = h-80/r+1/2.

So from the drawing above, we have distance from A to B:

using (1) above and using d = rt in the chart above, we 
have this system:



Since the 2nd equation is x = r, we replace x by r, and
simplify the other equations:



From the 1st equation we replace hr by r+y in the 2nd and 3rd equation,



They simplify to



From the 2nd equation, substituting 6r for y in the other two equations
gives 



Divide the 2nd equation through by 5



Substituting 6r-64 for z in the first equation.



   <-- answer

It isn't required, but if we get all the other variables,
h=7 hours, x = 16 miles, y=96 miles,
z=32 miles, so the distance from A to B is 112 miles.

 

Edwin

 
Ikleyn's solution is CORRECT.  I overlooked the word "MORE", and solved this
problem instead, where the "....." is below.  It is a much harder problem that
way.

Edwin