Question 1197607: Joseph traveled from Boston to Framingham at 50 mph and then back to Boston at 40 mph. what was Joseph's average speed on the round trip
Found 5 solutions by josgarithmetic, ewatrrr, greenestamps, ikleyn, math_tutor2020:
Answer by josgarithmetic(39628)   (Show Source): (Show Source):
You can put this solution on YOUR website!
SPEED TIME DISTANCE
B to F 50 d/50 d
F to B 40 d/40 d
ALL d/50+d/40 2d
average speed, round trip
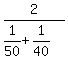
simplify and compute.
About 44 mph
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
D = rt 0r t = D/r
Let D represent the distance one-way
Time it takes to go to and from is the same ...
whether it be at varying speeds or at the average speed.
 Divide Thru by D
Let A be the average speed:
1/50 + 1/40 = 2/A
90/2000= 2/A
A = 2*(2000/90) = 44.4 mph rounded
Wish You the Best in your Studies. Divide Thru by D
Let A be the average speed:
1/50 + 1/40 = 2/A
90/2000= 2/A
A = 2*(2000/90) = 44.4 mph rounded
Wish You the Best in your Studies.
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other responses you have received use the same basic algebraic approach.
Here is an alternative method that I personally find easier.
The ratio of speeds is 50:40 = 5:4. Since the distances there and back are the same, the ratio of times spent at the two speeds is 4:5.
So 4/9 of the time was spent at 50mph and 5/9 of the time was spent at 40mph. The average speed is then
(4/9)50 + (5/9)40 = 200/9 + 200/9 = 400/9 = 44 4/9 mph
ANSWER: 44 4/9 miles per hour
Answer by ikleyn(52867)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Joseph traveled from Boston to Framingham at 50 mph and then back to Boston at 40 mph.
What was Joseph's average speed on the round trip?
~~~~~~~~~~~~~~~~~~~~
When the average velocities  and and  are given for each of the two parts of a round trip,
there is a standard formula to calculate the average speed are given for each of the two parts of a round trip,
there is a standard formula to calculate the average speed  of the total trip.
This formula is V = of the total trip.
This formula is V = 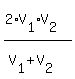 , and it gives the answer momentarily V = , and it gives the answer momentarily V = 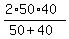 = = 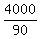 = 44 = 44  mph = 44.444 mph (rounded).
When you get such problem, it is expected that you know this formula and use it,
as well as it is expected that you know how to derive this formula.
Deriving is very simple.
If one way distance is D, then the time traveling with speed mph = 44.444 mph (rounded).
When you get such problem, it is expected that you know this formula and use it,
as well as it is expected that you know how to derive this formula.
Deriving is very simple.
If one way distance is D, then the time traveling with speed  is is  ,
while the time traveling with speed ,
while the time traveling with speed  is is  .
So, the total time of the two-ways round trip is .
So, the total time of the two-ways round trip is  + +  .
To find the average speed of the round trip, you divide total distance 2D by the total time .
To find the average speed of the round trip, you divide total distance 2D by the total time  + +  .
You get then
V = .
You get then
V = 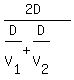 = cancel common factor D in the numerator and in the denominator = = cancel common factor D in the numerator and in the denominator = 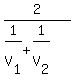 = simplify the fraction = = simplify the fraction = 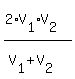 ,
as it was announced above.
You need to learn this formula and memorize it, and then you will be able to solve
hundreds similar problems mechanically, without any mental efforts.
When you get this level, it will mean that you know the method.
In addition, you will be able to teach other people (including your children and grand-children) on how to solve such problems
quickly, properly and in a right way. ,
as it was announced above.
You need to learn this formula and memorize it, and then you will be able to solve
hundreds similar problems mechanically, without any mental efforts.
When you get this level, it will mean that you know the method.
In addition, you will be able to teach other people (including your children and grand-children) on how to solve such problems
quickly, properly and in a right way.
Solved, with full explanations.
--------------
To see other similar solved problems, look into these lessons
- Calculating an average speed: a train going from A to B and back
- One more problem on calculating an average speed
in this site.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutors have provided great answers already.
Here's a numeric approach.
Let's say the distance from Boston to Framingham is 200 miles. Admittedly I'm not familiar with the Boston area, so this figure may be inaccurate compared to the real distance. But I'll stick to 200 since 50*40 = 200.
It doesn't matter what the distance is as the tutor @ikleyn has shown the distance (D) cancels.
The distance doesn't matter as long as the distance is the same from A to B, compared to from B to A.
Joseph traveled 200 miles from Boston to Framingham at 50 mph.
distance = rate*time
time = distance/rate
time = 200/50
time = 4 hours
Then he travels from Framingham back to Boston at 40 mph
We need to assume he takes the same route coming back home (or he'll likely travel a different distance).
time = distance/rate
time = 200/40
time = 5 hours
The total round trip distance is 200+200 = 400 miles.
The total time is 4+5 = 9 hours.
Ignore any moments where he is stopped, eg: getting gas, as that doesn't factor into the total travel time.
Then,
distance = rate*time
rate = distance/time
rate = 400/9
rate = 44.444 mph approximately
This represents the approximate average speed for the entire round trip.
A related concept is the harmonic mean
https://www.mathsisfun.com/numbers/harmonic-mean.html
|
|
|