Question 1183254: Mr. Trump drove to work in the morning at the average speed of 60 miles per hour. He returned home in the evening along the same route and averaged 45 miles per hour. To the nearest tenth, what is his average speed, in miles per hour, for the entire trip?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52775)   (Show Source):
You can put this solution on YOUR website! .
Mr. Trump drove to work in the morning at the average speed of 60 miles per hour.
He returned home in the evening along the same route and averaged 45 miles per hour.
To the nearest tenth, what is his average speed, in miles per hour, for the entire trip?
~~~~~~~~~~~~~~~~~~
There are two ways to solve the problem.
One way is to apply the ready to use formula for the average speed
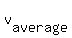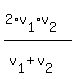 =  . (1)
It gives
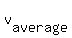=  = 51.4 miles per hour (rounded as requested). ANSWER
This way works ideally, if you know this formula (1).
If you DO NOT know it, you may DEDUCE this formula from the basic notions of Travel & Distance theory.
Let d be one way distance (the same in both directions).
Then the time driving to work is 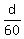 hours, and
the time driving back is  hours.
The average speed is the total distance, which is 2d, divided by the total time
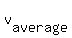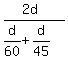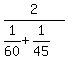=  = cancel d in the numerator and the denominator =  = = 51.4.
Naturally, you get the same answer.
The problem is just solved, and your horizon became just much wider, if you did not know these methods before.
My congratulations, and see the lessons
- Calculating an average speed: a train going from A to B and back
- One more problem on calculating an average speed
in this site.
Find there many other similar solved problems.
//////////////
The post-solution note
All commonly used ways/methods of solving such and similar problems
rotate around the formula (1) - use you it directly or deduce as I showed it in my solution.
Therefore, it is VERY USEFUL to you to know it and to apply appropriately.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
There are in fact many more than two ways to solve a problem like this....
Here is what I would do to solve this, given that the two speeds are "nice" numbers.
The distances to and from work are of course the same, and the ratio of the two speeds is 60:45 = 4:3. That means the ratio of times spent at the two speeds is 3:4. So 3/7 of the time he drove at 60mph and 4/7 of the time he drove at 45mph.
Since average speed is total distance divided by total time, his average speed in mph was
ANSWER: his average speed in mph was 360/7 = 51 3/7 or 51.4, to the nearest tenth.
|
|
|
