Question 1179659: Flying with the wind, a plane flew 1,120 mi in 4 h. Against the wind, the plane required 7 h to fly the same distance. Find the rate of the plane in calm air and the rate of the wind.
Found 4 solutions by mananth, MathTherapy, ikleyn, n2:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! Plane speed =x mph in still air
wind speed =y mph
against wind x-y 7.00 hours
with wind x+y 4.00 hours
Distance = same= 1120 miles
t=d/r
1120 / ( x - y )= 7.00
1120.00 /( x + y) = 4.00
1 x -1 y = 160.00 ....................1
1120 / ( x+ 1 y )= 4.00
1120.00 /( x - 1 y) = 4.00
1.00 x + 1.00 y = 280.00 ...............2
Multiply (1) by 1.00
Multiply (2) by 1.00
we get
1 x + 1 y = 160
1 x - 1 y = 280
2 x = 440
/ 2
x = 220 mph
plug value of x in (1)
1 x -1.00 y = 160.00
220 -1.00 y = 160.00
- y = 160 -220
- y = -60
y = 60 mph
Answer by MathTherapy(10719)  (Show Source):
You can put this solution on YOUR website!
Flying with the wind, a plane flew 1,120 mi in 4 h. Against the wind, the plane required 7 h to fly the same distance. Find the rate of the plane in calm air and the rate of the wind.
That MUMBO-JUMBO method by the other person is RIDICULOUS! I hope you're not planning on using it. If not, then read on.
Let the speed in still air, and speed of wind be S, and W, respectively
Then we get the following system of TOTAL-SPEED equations:  ====> 
Now, add the 2 equations and solve for S to get the plane's speed in still air.
Afterwards, substitute the value of S into either eq (i) or (ii) and solve for W to get the wind-speed.
Answer by ikleyn(53618)  (Show Source):
You can put this solution on YOUR website! .
Flying with the wind, a plane flew 1,120 mi in 4 h.
Against the wind, the plane required 7 h to fly the same distance.
Find the rate of the plane in calm air and the rate of the wind.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u be the rate of the plane at no wind (in miles per hour)
and v be the rate of the wind (in the same units).
Then the effective rate of the plane with the wind is u + v
and the effective rate of the plane against the wind is u - v.
From the problem, the effective rate of the plane with the wind is the distance of 1120 miles
divided by the time of 4 hours {{1120/4}}} = 280 mph.
The effective rate of the plane against the wind is the distance of 1120 miles
divided by the time of 7 hours 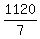 = 160 mph.
So, we have two equations to find 'u' and 'v'
u + v = 280, (1)
u - v = 160. (2)
To solve, add equations (1) and (2). The terms 'v' and '-v' will cancel each other, and you will get
2u = 280 + 160 = 440 ---> u = 440/2 = 220.
Now from equation (1)
v = 280 - u = 280 - 220 = 60.
ANSWER. The rate of the plane in still air is 220 mph. The rate of the wind is 60 mph km/h.
Solved.
-------------------------------
My solution produces the same answer as in the post by @mananth, but makes it in clean, clear and correct form,
while calculations in the post by @mananth contradict to each other literally in every line.
We, the tutors, write here our solutions not only to get certain numerical answer.
We write to teach - and, in particular, to teach writing solutions in accurate and clear style.
@mananth repeats his construction of solution with no change for all similar problems on flies
with and against the wind simply because his COMPUTER CODE is written this way.
But his computer code is written in a bad style. It is simply DEFECTIVE.
But @mananth does not change it just during several ( five or seven or even more ) years.
My impression of his writing is that he does not read what his code produces, because it is not interesting to him.
To me, it is monstrous style posting to the forum.
Answer by n2(54)  (Show Source):
You can put this solution on YOUR website! .
Flying with the wind, a plane flew 1,120 mi in 4 h.
Against the wind, the plane required 7 h to fly the same distance.
Find the rate of the plane in calm air and the rate of the wind.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u be the rate of the plane at no wind (in miles per hour)
and v be the rate of the wind (in the same units).
Then the effective rate of the plane with the wind is u + v
and the effective rate of the plane against the wind is u - v.
From the problem, the effective rate of the plane with the wind is the distance of 1120 miles
divided by the time of 4 hours {{1120/4}}} = 280 mph.
The effective rate of the plane against the wind is the distance of 1120 miles
divided by the time of 7 hours 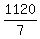= 160 mph.
So, we have two equations to find 'u' and 'v'
u + v = 280, (1)
u - v = 160. (2)
To solve, add equations (1) and (2). The terms 'v' and '-v' will cancel each other, and you will get
2u = 280 + 160 = 440 ---> u = 440/2 = 220.
Now from equation (1)
v = 280 - u = 280 - 220 = 60.
ANSWER. The rate of the plane in still air is 220 mph. The rate of the wind is 60 mph km/h.
Solved.
|
|
|
