Question 1179658: A plane traveling with the wind flew 1312.5 mi in 5.25 h. Against the wind, the plane required 6.25 h to fly the same distance. Find the rate of the plane in calm air and the rate of the wind.
Found 5 solutions by mananth, MathTherapy, josgarithmetic, ikleyn, n2:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! A plane traveling with the wind flew 1312.5 mi in 5.25 h. Against the wind, the plane required 6.25 h to fly the same distance.
Plane speed =x mph in still air
wind speed =y mph
against wind x-y 6.25 hours
with wind x+y 5.25 hours
Distance = same= 1312.5 miles
t=d/r
1312.5 / ( x - y )= 6.25
1120.00 /( x + 1 y) = 5.25
1.00 x 1.00 y = 179.20 ....................1
1312.5 / ( x- 1 y )= 5.25
1312.50 /( x - 1 y) = 5.25
1.00 x - 1.00 y = 250.00 ...............2
Multiply (1) by 1.00
Multiply (2) by 1.00
we get
1 x + 1 y = 179.2
1 x - 1 y = 250
2 x = 429.2
/ 2
x = 214.6 mph
Answer by MathTherapy(10719)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A plane traveling with the wind flew 1312.5 mi in 5.25 h. Against the wind, the plane required 6.25 h to fly the same distance. Find the rate of the plane in calm air and the rate of the wind.
Same MUMBO-JUMBU method by this person, and now, a WRONG answer. IGNORE it ALL!!
Use the method I pointed out earlier. It will not only be MUCH easier but you'll get the correct answer.
Answer by josgarithmetic(39736)   (Show Source): (Show Source):
Answer by ikleyn(53618)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A plane traveling with the wind flew 1312.5 mi in 5.25 h.
Against the wind, the plane required 6.25 h to fly the same distance.
Find the rate of the plane in calm air and the rate of the wind.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @mananth is incorrect: it has arithmetic errors.
Not only is it technically unsuitable, but it is also unsuitable in its design.
In this my post, I provide short and straightforward solution to the given problem.
Let x be the rate of the plane in calm air, in miles per hour.
Let y be the rate of the wind.
Then the effective speed of the plane with the wind is (x+y) mph,
while the effective speed of the plane against the wind is (x-y) mph,
From the problem, the effective rate of the plane with the wind is the distance divided by the travel time
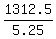 = 250 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time = 250 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time
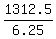 = 210 miles per hour.
So, we have these two equations
x + y = 250 (1)
x - y = 210 (2)
To find x, add the equation. You will get
2x = 250 + 210 = 460, x = 460/2 = 230.
Now express y from equation (1) and calculate
y = 250 - x = 250 - 230 = 20.
At this point the problem is solved completely.
ANSWER. The speed of the plane in calm air is 230 mph. The rate of the wind is 20 mph. = 210 miles per hour.
So, we have these two equations
x + y = 250 (1)
x - y = 210 (2)
To find x, add the equation. You will get
2x = 250 + 210 = 460, x = 460/2 = 230.
Now express y from equation (1) and calculate
y = 250 - x = 250 - 230 = 20.
At this point the problem is solved completely.
ANSWER. The speed of the plane in calm air is 230 mph. The rate of the wind is 20 mph.
Solved.
----------------------------
I placed this my solution here as an opposite alternative to the solution by @mananth.
Now I will explain you, why I think that my solution is better than that of @mananth.
The @mananth solution is more long way reasoning and calculations than it is necessary.
My solution is straightforward and contains only necessary reasoning and calculations.
Everything which is not effective and straightforward, is filtered out.
The school education always prefers more straightforward and short reasoning, explanations and calculations,
because the goal of solving such problems is not only getting a correct answer.
A true goal of solving such problems is to teach students to organize
and present their thoughts and their arguments in adequate form.
@mananth does it his way only because his computer code, which he permanently uses to create the solution file,
is written this way - but his way is not effective.
It is why I prepared and placed here my solution to provide a better way
for you, a reader, to learn and to master this subject.
What I wrote here are not empty words.
Today, on Jan.21, 2026 I looked on how artificial intelligence treats this problem.
The Google AI Overflow repeats this long process, copying the style of @mananth.
Thus, thousands of schoolchildren will suffer and will not know how to correctly present
their thoughts and how to correctly present a solutions to such problems.
And this is already a national-scale problem - when AI is copying from badly written sources.
Answer by n2(54)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A plane traveling with the wind flew 1312.5 mi in 5.25 h.
Against the wind, the plane required 6.25 h to fly the same distance.
Find the rate of the plane in calm air and the rate of the wind.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the rate of the plane in calm air, in miles per hour.
Let y be the rate of the wind.
Then the effective speed of the plane with the wind is (x+y) mph,
while the effective speed of the plane against the wind is (x-y) mph,
From the problem, the effective rate of the plane with the wind is the distance divided by the travel time
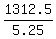 = 250 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time = 250 miles per hour,
and the effective rate of the plane against the wind is the distance divided by the travel time
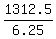 = 210 miles per hour.
So, we have these two equations
x + y = 250 (1)
x - y = 210 (2)
To find x, add the equation. You will get
2x = 250 + 210 = 460, x = 460/2 = 230.
Now express y from equation (1) and calculate
y = 250 - x = 250 - 230 = 20.
At this point the problem is solved completely.
ANSWER. The speed of the plane in calm air is 230 mph. The rate of the wind is 20 mph. = 210 miles per hour.
So, we have these two equations
x + y = 250 (1)
x - y = 210 (2)
To find x, add the equation. You will get
2x = 250 + 210 = 460, x = 460/2 = 230.
Now express y from equation (1) and calculate
y = 250 - x = 250 - 230 = 20.
At this point the problem is solved completely.
ANSWER. The speed of the plane in calm air is 230 mph. The rate of the wind is 20 mph.
Solved.
|
|
|