SOLUTION: It's 90 miles from Ayville to Beeville. It's another 195 miles from Beeville to Charleston. Chad drives 20 miles per hour faster from Beeville to Charleston than from Ayville to Be

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: It's 90 miles from Ayville to Beeville. It's another 195 miles from Beeville to Charleston. Chad drives 20 miles per hour faster from Beeville to Charleston than from Ayville to Be      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1175351: It's 90 miles from Ayville to Beeville. It's another 195 miles from Beeville to Charleston. Chad drives 20 miles per hour faster from Beeville to Charleston than from Ayville to Beeville. If his combined travel time is 5 hours, what are his average speeds?
Speed from Ayville to Beeville:?
Speed from Beeville to Charleston:?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39614) About Me  (Show Source):
You can put this solution on YOUR website!
            SPEED       TIME           DIST.
AtoB        r           90/r            90
BtoC        r+20        195/(r+20)      195
TOTAL                    5

Continue with equation 90%2Fr%2B195%2F%28r%2B20%29=5, and solve it for r,...

Answer by ikleyn(52756) About Me  (Show Source):
You can put this solution on YOUR website!
.

The time equation is


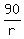    90%2Fr + 195%2F%28r%2B20%29 = 5 hours.


The solution you can guess mentally:  r = 45 km/h from A to B.


Then the average speed from B to C is 45+20 = 65 km/h.



By the way, notice that the left side of the equation is the function of "r", 

monotonically decreasing with variable "r" in positive domain.


So, if you guess one solution, you can be sure that this solution is UNIQUE and there is NO other solution.


So, such "guessing", accompanied with noticing about monotonicy is logically absolutely strict way to solve the problem.



Alternatively, you may reduce the problem to quadratic equation and solve it.



In any case, from my post you just know the answer.