A cistern can be filled by two pipes. The small pipe alone will take 24 minutes
longer than the larger pipe to fill the cistern alone. The small pipe alone will take 32 minutes longer to fill the cistern alone than when the two pipes are operating together. How long will it take the larger pipe to fill the cistern alone
Let time it takes large pipe to fill cistern, be L
Then, large pipe can to fill 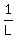 of cistern, in 1 minute
Also, time it takes small pipe to fill cistern = L + 24
Thus, small pipe can fill
of cistern, in 1 minute
Also, time it takes small pipe to fill cistern = L + 24
Thus, small pipe can fill 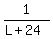 of cistern in 1 minute
In addition, time taken by both to fill cistern: L + 24 - 32, or L - 8
Therefore, both pipes can fill
of cistern in 1 minute
In addition, time taken by both to fill cistern: L + 24 - 32, or L - 8
Therefore, both pipes can fill 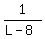 of cistern in 1 minute
We then get:
of cistern in 1 minute
We then get:  (L + 24)(L - 8) + L(L - 8) = L(L + 24) -------- Multiplying by LCD, L(L + 24)(L - 8)
(L + 24)(L - 8) + L(L - 8) = L(L + 24) -------- Multiplying by LCD, L(L + 24)(L - 8)
 (L - 24)(L + 8) = 0
Time it takes larger pipe to fill cistern, or
(L - 24)(L + 8) = 0
Time it takes larger pipe to fill cistern, or  OR L = - 8 (ignore)
You can do the CHECK!!
OR L = - 8 (ignore)
You can do the CHECK!!