Question 1166452: A motorboat accelerates uniformly from a velocity of 6.7 m/s to the west to a velocity of 1.4 m/s to the west. If its acceleration was 3.4 m/s^2 to the east,
how far did it travel during the acceleration? Answer in units of m.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2138)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a problem in one-dimensional kinematics that can be solved using the time-independent equation relating velocity, acceleration, and displacement.
## 📐 Kinematics Calculation
1. **Define Direction and Variables:**
Let **West be the positive direction** ($+$).
* Initial Velocity ($\vec{v}_i$): $6.7 \text{ m/s}$ West $\implies v_i = +6.7 \text{ m/s}$
* Final Velocity ($\vec{v}_f$): $1.4 \text{ m/s}$ West $\implies v_f = +1.4 \text{ m/s}$
* Acceleration ($\vec{a}$): $3.4 \text{ m/s}^2$ East $\implies a = -3.4 \text{ m/s}^2$
2. **Select the Kinematic Equation:**
Since the time is not given, we use the equation that relates the final velocity, initial velocity, acceleration, and displacement ($\Delta x$):
$$v_f^2 = v_i^2 + 2a \Delta x$$
3. **Solve for Displacement ($\Delta x$):**
$$\Delta x = \frac{v_f^2 - v_i^2}{2a}$$
4. **Substitute Values and Compute:**
$$\Delta x = \frac{(1.4 \text{ m/s})^2 - (6.7 \text{ m/s})^2}{2(-3.4 \text{ m/s}^2)}$$
$$\Delta x = \frac{1.96 \text{ m}^2/\text{s}^2 - 44.89 \text{ m}^2/\text{s}^2}{-6.8 \text{ m/s}^2}$$
$$\Delta x = \frac{-42.93 \text{ m}^2/\text{s}^2}{-6.8 \text{ m/s}^2}$$
$$\Delta x \approx 6.3132 \text{ m}$$
The distance traveled is the magnitude of the displacement.
The distance the motorboat traveled during the acceleration is **$6.31$ m**.
Answer by ikleyn(53427)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A motorboat accelerates uniformly from a velocity of 6.7 m/s to the west
to a velocity of 1.4 m/s to the west.
If its acceleration was 3.4 m/s^2 to the east, how far did it travel during the acceleration?
Answer in units of m.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Here is my alternative solution.
The time of accelerating (which is deceleration, actually), is the difference of speeds
divided by the deceleration value
t = 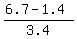 = 1.558823529 seconds.
The distance traveled by the motorboat during this time is the average speed times time 't'
distance = = 1.558823529 seconds.
The distance traveled by the motorboat during this time is the average speed times time 't'
distance = 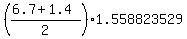 = 6.313235294 meters.
Rounding, you get the ASNSWER: the distance is about 6.31 meters. = 6.313235294 meters.
Rounding, you get the ASNSWER: the distance is about 6.31 meters.
Solved.
|
|
|