Question 1163678: Jerry and Kenny start running from two difference points which are 100 meters away on a circular track with length 400 meters. They both run clockwise. Jerry runs at 5 m/s, and Kenny runs at 4 m/s. Each of them takes a break for 10 seconds every 100 meters. How long will Jerry catch up with Kenny?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem is deficient; the statement that they both run clockwise doesn't tell us anything.
If, at the start, Jerry is 100 meters "behind" Kenny on the 400 meter track, then he has to make up 100 meters to catch up; but if he is already 100 meters "ahead" of Kenny, then he has to make up 300 meters to catch up.
Re-post the problem, making the problem clear.
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Jerry and Kenny start running simultaneously from two different points which are 100 meters away on a circular track with length 400 meters.
They both run clockwise. Jerry runs at 5 m/s, and Kenny runs at 4 m/s. Each of them takes a break for 10 seconds every 100 meters.
How long will Jerry catch up with Kenny?
~~~~~~~~~~~~~~~
As the problem is worded, printed, posted and presented, it has a deficiency to be ambiguous.
To take this ambiguity off, I will reformulate it in this way:
Jerry and Kenny start running from two different points on a circular track with length 400 meters.
They both run clockwise, and Kenny has headstart of 100 meters. Jerry runs at 5 m/s, and Kenny runs at 4 m/s.
Each of them takes a break for 10 seconds every 100 meters. How long will Jerry catch up with Kenny?
Now I am ready to solve the problem.
In this problem, the key to the solution is to find the way/(the method) to analyze, the way to organize thoughts and
the way to present the results.
Each of the two runners runs cyclically.
The cycle by Jerry is to run 100 m in 20 seconds; then to rest 10 seconds. So, his cycle is 30 seconds long.
The cycle by Kenny is to run 100 m in 25 seconds; then to rest 10 seconds. So, his cycle is 35 seconds long.
I will analyze their positions (as the time and the coordinate along the circumference, beginning from Kerry's starting point)
at the end of the each runner cycle.
Notice and memorize that Jerry is faster.
For Jerry, time 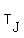 = 30*(i-1) and position = 30*(i-1) and position 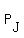 = -100 + 100*(i-1), "i" is the number of cycle.
For Kenny, time = -100 + 100*(i-1), "i" is the number of cycle.
For Kenny, time  = 35*(i-1) and position = 35*(i-1) and position  = 100*(i-1), "i" is the number of cycle.
Jerry first time will catch up with Kenny, when their cycles will have common ending time AND the positions will be the same
or will differ by a multiple of the length of the circumference.
Since 30 = 5*6 and 35 = 5*7, the first candidate to check is the 7-th cycle for Jerry and the 6-th cycle for Kenny.
And if you will calculate their time-space coordinates at the end of their corresponding circles,
you will see that they are at the same time-space point at the time t= 210 seconds and the coordinate on the circle 600 meters,
which is the same as 200 m away along the circle clockwise from the Kenny starting point.
Since t = 210 seconds is the end of the Jerry's 10-second resting period and the end of the Kenny's 10-second resting period,
it means, that ACTUALLY Jerry will catch up Kenny first time at the time moment t= 210-10 = 200 second after start running.
ANSWER. Jerry will catch Kenny in 200 seconds. = 100*(i-1), "i" is the number of cycle.
Jerry first time will catch up with Kenny, when their cycles will have common ending time AND the positions will be the same
or will differ by a multiple of the length of the circumference.
Since 30 = 5*6 and 35 = 5*7, the first candidate to check is the 7-th cycle for Jerry and the 6-th cycle for Kenny.
And if you will calculate their time-space coordinates at the end of their corresponding circles,
you will see that they are at the same time-space point at the time t= 210 seconds and the coordinate on the circle 600 meters,
which is the same as 200 m away along the circle clockwise from the Kenny starting point.
Since t = 210 seconds is the end of the Jerry's 10-second resting period and the end of the Kenny's 10-second resting period,
it means, that ACTUALLY Jerry will catch up Kenny first time at the time moment t= 210-10 = 200 second after start running.
ANSWER. Jerry will catch Kenny in 200 seconds.
Solved.
|
|
|