Question 1163674: If Albert rides a bike from City A to City B, and he takes 6 hours for the entire trip. If Bob rides a bike from City B to City A, and he takes 4 hours for the trip assuming they are on the same road. If Albert leaves City A and Bob leaves City B at the same time toward to each other, when they meet, the place is 2 km away from the halfway. After they arrives their own destination, they turn around, and continue to ride. When they meet the second time, how far is the place is away from the place they meet the first time?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Albert rides a bike from City A to City B, and he takes 6 hours for the entire trip.
If Bob rides a bike from City B to City A, and he takes 4 hours for the trip assuming they are on the same road.
If Albert leaves City A and Bob leaves City B at the same time toward to each other, when they meet, the place is 2 km away from the halfway.
:
A->-------*----2----|----------------<-B
Use this to find the distance from A to B
let x = halfway, the the dist from A to B = 2x
then
a's speed = 2x/6 = x/3 km/hr and b's speed = 2x/4 = x/2 km/hr
a travels x-2 km while b travels x+2; time = dist/speed
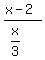 = = 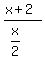
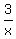 (x-2) = (x-2) = 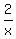 (x+2) (x+2)
therefore
3(x-2) = 2(x+2)
3x - 6 = 2x + 4
3x - 2x = 4 + 6
x = 10, the distance from A to B = 20 km
a's speed: 20/6 = 3.33 km/hr; b's speed: 20/4 = 5 km/hr
:
:
After they arrives their own destination, they turn around, and continue to ride.
When they meet the second time, how far is the place is away from the place they meet the first time
:
When a reaches city B, b will have turned around and rode 2 hrs toward a which is 2*5 = 10 km or half way
(their 10 km apart when a starts back towards A)
let t = time for them to meet at this point in time
3.33t + 5t = 10
8.33t = 10
t = 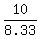
t = 1.2 hrs
therefore b will be 1.2(5) = 6 km passed the halfway point
the other point at which they met is 2 km on the other side of the halfway point
therefore
2 + 6 = 8 km between the two meeting points
|
|
|