Question 1163673: Sam drives from City A to City B, and Richard drives from City B to City A on the same road. When they meet, Sam has driven 120 km. They continue to drive to their own destination. When they arrive at their destination, they turn around and continue to drive. When they meet the second time, the place is 1/5 of the distance between the two cities away from City B. What is the distance between the two cities?
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Sam drives from City A to City B, and Richard drives from City B to City A on the same road. When they meet, Sam has driven 120 km.
They continue to drive to their own destination. When they arrive at their destination, they turn around and continue to drive.
When they meet the second time, the place is 1/5 of the distance between the two cities away from City B.
What is the distance between the two cities?
Solution
The scheme of placing points is shown in the Figure below.
+--------------------------------|-----------|--------------+
A M F B
Points A and B are cities; point M is the 1st meeting point; point F is the 2-nd meeting point.
So, AM = 120 kilometers.
Let x be the distance from the 1st meeting point to B.
Thus the total distance is 120+x kilometers.
The times driving from the starting points to the 1st meeting pojnt are the same
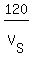 = = 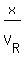 , (1)
where , (1)
where  and and  are the rates of Sam and Richard, respective.
It is our first equation, which I want to rewrite in this form as the ratio of their rates are the rates of Sam and Richard, respective.
It is our first equation, which I want to rewrite in this form as the ratio of their rates
 = = 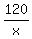 . (2)
The distance Sam drove from the 1st meeting point to the second meeting point was . (2)
The distance Sam drove from the 1st meeting point to the second meeting point was 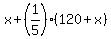 km.
The time Sam spent covering this distance was km.
The time Sam spent covering this distance was  = = 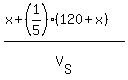 hours.
The distance Richard drove from the 1st meeting point to the second meeting point was hours.
The distance Richard drove from the 1st meeting point to the second meeting point was 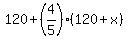 km.
The time Richard spent covering this distance was km.
The time Richard spent covering this distance was  = = 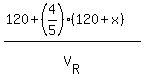 hours.
The times hours.
The times  and and  are the same; it leads to equation are the same; it leads to equation
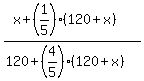 = =  .
In the right side, replace .
In the right side, replace  by by 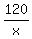 , based on (2). You will get then , based on (2). You will get then
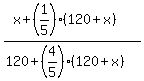 = = 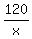 .
Simplify it step by step .
Simplify it step by step
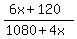 = = 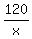
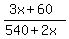 = = 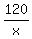 x*(3x + 60) = 120*(540+2x)
3x^2 + 60x = 120*540 + 240x
3x^2 - 180x - 120*540 = 0
x^2 - 60x - 21600 = 0
(x+120)*(x-180) = 0
Of the two roots, -120 and 180, only positive 180 makes sense.
So, the distance x is 180 kilometers, and the total distance from A to B is 120+180 = 300 kilometers. ANSWER
x*(3x + 60) = 120*(540+2x)
3x^2 + 60x = 120*540 + 240x
3x^2 - 180x - 120*540 = 0
x^2 - 60x - 21600 = 0
(x+120)*(x-180) = 0
Of the two roots, -120 and 180, only positive 180 makes sense.
So, the distance x is 180 kilometers, and the total distance from A to B is 120+180 = 300 kilometers. ANSWER
Solved.
---------------
Surely, this problem is two levels higher than a regular Math/Physics problem in any high school.
It is, actually, an Olympiad level problem in Physics.
Could you tell me please where is it from, from which source ?
Do not forget to post your "THANKS" to me for my teaching.
|
|
|